3. d-separation, Graph Transformation

In a different place, we talked about direction-dependent separation, or d-separation. In this notebook, we will explore a different way to compute d-separation based on graph transformation.

3.1. Graph example

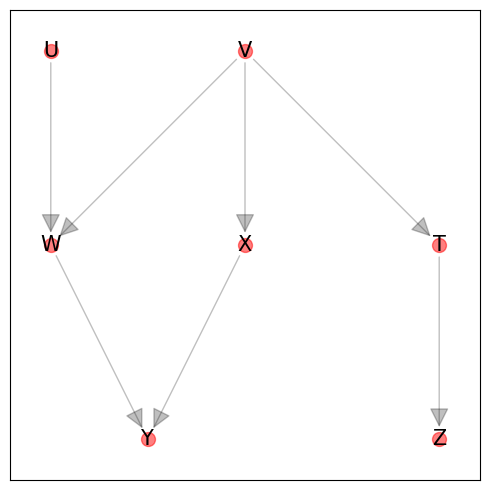
Here is a graph taken from this most excellent video tutorial on d-separation exercises. We will be using this graph to show some d-separation queries.

import networkx as nx
from collections import namedtuple

Graph = namedtuple('Graph', 'u, d')

def get_edges(s):
    edges = s.split('\n')
    edges = map(lambda line: line.split('->'), edges)
    edges = map(lambda tokens: tuple([t.strip() for t in tokens]), edges)
    edges = list(edges)

    return edges

def get_directed_graph(edges):
    g = nx.DiGraph()
    g.add_edges_from(edges)

    return g

def get_undirected_graph(edges):
    g = nx.Graph()
    g.add_edges_from(edges)

    return g

def get_graph(s):
    e = get_edges(s)

    d = get_directed_graph(e)
    u = get_undirected_graph(e)
    g = Graph(u, d)

    return g

s = '''
U -> W
V -> W
V -> X
V -> T
W -> Y
X -> Y
T -> Z
'''.strip()

g = get_graph(s)

import matplotlib.pyplot as plt

pos = nx.nx_agraph.graphviz_layout(g.d, prog='dot')

fig, ax = plt.subplots(figsize=(5, 5))

nx.draw_networkx_nodes(
    G=g.d,
    pos=pos,
    ax=ax,
    node_size=100,
    alpha=0.5,
    node_color='red'
)

nx.draw_networkx_labels(
    G=g.d,
    pos=pos,
    ax=ax,
    font_size=15,
    font_color='black',
    alpha=1.0
)

nx.draw_networkx_edges(
    G=g.d,
    pos=pos,
    alpha=0.25,
    arrowsize=30,
    ax=ax
)

fig.tight_layout()

3.2. Algorithm

Here’s the graph transformation algorithm to determine if \(X\) and \(Y\) are d-separated given \(Z\).

• Input:

  • \(G\): DAG

  • \(X\): start node

  • \(Y\): end node

  • \(Z\): evidence nodes

• Output: True or False

• Create the ancestral graph \(A\) from \(G\) (using the starting nodes in \(X, Y, Z\))

• Create the moralized graph \(M\) from \(A\)

• Create the dependency graph \(D\) from \(M\) by remove all nodes in \(Z\) and their associated edges

• If there is no path between \(X\) and \(Y\) in \(D\), return true, else false

import itertools

def get_ancestral_graph(g, x, y, z):
    seen = []
    nodes = [x, y] + list(z)

    while True:
        seen = seen + [n for n in nodes if n not in seen]

        parents = [list(g.d.predecessors(n)) for n in nodes]
        parents = itertools.chain(*parents)
        parents = set(parents)
        parents = parents - set(seen)
        parents = list(parents)

        if len(parents) < 1:
            break
        else:
            nodes = parents

    a = g.u.copy()
    for n in g.u.nodes():
        if n not in seen:
            a.remove_node(n)
    return a

def get_moralized_graph(g, a, x, y, z):
    m = a.copy()

    for n in a.nodes():
        pa_links = itertools.combinations(list(g.d.predecessors(n)), 2)
        for pa_1, pa_2 in pa_links:
            if pa_1 in m.nodes() and pa_2 in m.nodes() and not m.has_edge(pa_1, pa_2):
                m.add_edge(pa_1, pa_2)

    return m

def get_dependency_graph(m, evidence=set()):
    d = m.copy()

    for n in evidence:
        d.remove_node(n)

    return d

def is_d_separated(g, x, y, evidence=set()):
    a = get_ancestral_graph(g, x, y, evidence)
    m = get_moralized_graph(g, a, x, y, evidence)
    d = get_dependency_graph(m, evidence)

    if x not in d.nodes() or y not in d.nodes() or not nx.has_path(d, x, y):
        return True
    return False

3.3. Examples

Below are some exercise examples to query for d-separation based on the algorithm and code above.

3.3.1. Example 1

False == is_d_separated(g, 'V', 'Z')

True

3.3.2. Example 2

True == is_d_separated(g, 'V', 'Z', {'T'})

True

3.3.3. Example 3

True == is_d_separated(g, 'U', 'V')

True

3.3.4. Example 4

False == is_d_separated(g, 'U', 'V', {'W'})

True

3.3.5. Example 5

True == is_d_separated(g, 'U', 'V', {'X'})

True

3.3.6. Example 6

False == is_d_separated(g, 'U', 'V', {'Y'})

True

3.3.7. Example 7

True == is_d_separated(g, 'U', 'V', {'Z'})

True

3.3.8. Example 8

False == is_d_separated(g, 'W', 'X')

True

3.3.9. Example 9

True == is_d_separated(g, 'X', 'T', {'V'})

True

3.3.10. Example 10

False == is_d_separated(g, 'X', 'W', {'U'})

True

3.3.11. Example 11

False == is_d_separated(g, 'Y', 'Z')

True

3.3.12. Example 12

True == is_d_separated(g, 'Y', 'Z', 'T')

True

3.3.13. Example 13 **

False == is_d_separated(g, 'Y', 'Z', {'X'})

True

3.3.14. Example 14

True == is_d_separated(g, 'Y', 'Z', {'V'})

True

3.3.15. Example 15

True == is_d_separated(g, 'W', 'Z', {'V'})

True

3.3.16. Example 16

True == is_d_separated(g, 'U', 'Z')

True

3.3.17. Example 17

False == is_d_separated(g, 'U', 'Z', {'Y'})

True

3.3.18. Additional examples

False == is_d_separated(g, 'U', 'W')

True

True == is_d_separated(g, 'U', 'W', {'U'})

True

True == is_d_separated(g, 'U', 'W', {'W'})

True