10. Log-Linear Models and Graphical Models

For any three categorical variables A, B and C, with corresponding I, J and K levels, there are 9 log-linear model LLM specifications possible. These 9 LLM specifications can be grouped into the 5 broad categories of

  • independence (also called complete independence),

  • joint independence (also called block independence),

  • conditional independence (also called partial independence),

  • homogenous association (also called uniform association) or

  • saturated.

Specifically, the functional specifications are written as follows.

  • independence: A, B and C are all independent, denoted as (A, B, C)

    • \(\log{\mu_{ijk}} = \lambda + \lambda_i^A + \lambda_j^B + \lambda_k^C\)

  • joint independence: AB are jointly independent of C (AB, C); AC are jointly independent of B (AC, B); BC are jointly independent of A (BC, A)

    • \(\log{\mu_{ijk}} = \lambda + \lambda_i^A + \lambda_j^B + \lambda_k^C + \lambda_{jk}^{AB}\)

    • \(\log{\mu_{ijk}} = \lambda + \lambda_i^A + \lambda_j^B + \lambda_k^C + \lambda_{jk}^{AC}\)

    • \(\log{\mu_{ijk}} = \lambda + \lambda_i^A + \lambda_j^B + \lambda_k^C + \lambda_{jk}^{BC}\)

  • conditional independence: A and B are independent given C (AC, BC); A and C are independent given B (AB, BC); B and C are independent give A (AB, AC)

    • \(\log{\mu_{ijk}} = \lambda + \lambda_i^A + \lambda_j^B + \lambda_k^C + \lambda_{ik}^{AC} + \lambda_{jk}^{BC}\)

    • \(\log{\mu_{ijk}} = \lambda + \lambda_i^A + \lambda_j^B + \lambda_k^C + \lambda_{ij}^{AB} + \lambda_{jk}^{BC}\)

    • \(\log{\mu_{ijk}} = \lambda + \lambda_i^A + \lambda_j^B + \lambda_k^C + \lambda_{ij}^{AB} + \lambda_{ik}^{AC}\)

  • homogeneous association: there is no three way interaction (AB, AC, BC)

    • \(\log{\mu_{ijk}} = \lambda + \lambda_i^A + \lambda_j^B + \lambda_k^C + \lambda_{ij}^{AB} + \lambda_{ik}^{AC} + \lambda_{jk}^{BC}\)

  • saturated: there are main, pairwise and three-way effects (ABC)

    • \(\log{\mu_{ijk}} = \lambda + \lambda_i^A + \lambda_j^B + \lambda_k^C + \lambda_{ij}^{AB} + \lambda_{ik}^{AC} + \lambda_{jk}^{BC} + \lambda_{ijk}^{ABC}\)

Each of these models have a corresponding graphical representation as follows.

[1]:

import networkx as nx
import numpy as np
import matplotlib.pyplot as plt

plt.style.use('seaborn')

def get_graph(nodes=['A', 'B', 'C'], edges=[]):
    g = nx.Graph()

    for n in nodes:
        g.add_node(n)
    for u, v in edges:
        g.add_edge(u, v)

    return g

def draw_graph(k, g, ax):
    pos = {
        'A': (200, 250),
        'B': (150, 230),
        'C': (250, 230)
    }

    params = {
        'node_color': 'r',
        'node_size': 350,
        'node_shape': 's',
        'alpha': 0.5,
        'pos': pos,
        'ax': ax
    }
    _ = nx.drawing.nx_pylab.draw_networkx_nodes(g, **params)

    params = {
        'font_size': 15,
        'font_color': 'k',
        'font_family': 'monospace',
        'pos': pos,
        'ax': ax
    }
    _ = nx.drawing.nx_pylab.draw_networkx_labels(g, **params)

    params = {
        'width': 1.5,
        'alpha': 0.5,
        'edge_color': 'b',
        'arrowsize': 20,
        'pos': pos,
        'ax': ax
    }
    _ = nx.drawing.nx_pylab.draw_networkx_edges(g, **params)

    ax.set_title(k)
    ax.grid(False)

graphs = {
    '(A,B,C)': [],
    '(A,BC)': [('B', 'C')],
    '(B,AC)': [('A', 'C')],
    '(C,AB)': [('A', 'B')],
    '(AC,CB)': [('A', 'C'), ('C', 'B')],
    '(AB,BC)': [('A', 'B'), ('B', 'C')],
    '(BA,AC)': [('B', 'A'), ('A', 'C')],
    '(AB, AC, BC)': [('A', 'B'), ('B', 'C'), ('A', 'C')]
}

graphs = {k: get_graph(edges=edges) for k, edges in graphs.items()}

fig, axes = plt.subplots(2, 4, figsize=(15, 7))
axes = np.ravel(axes)

for (k, g), ax in zip(graphs.items(), axes):
    draw_graph(k, g, ax)

fig.patch.set_facecolor('#fca100')
plt.tight_layout()
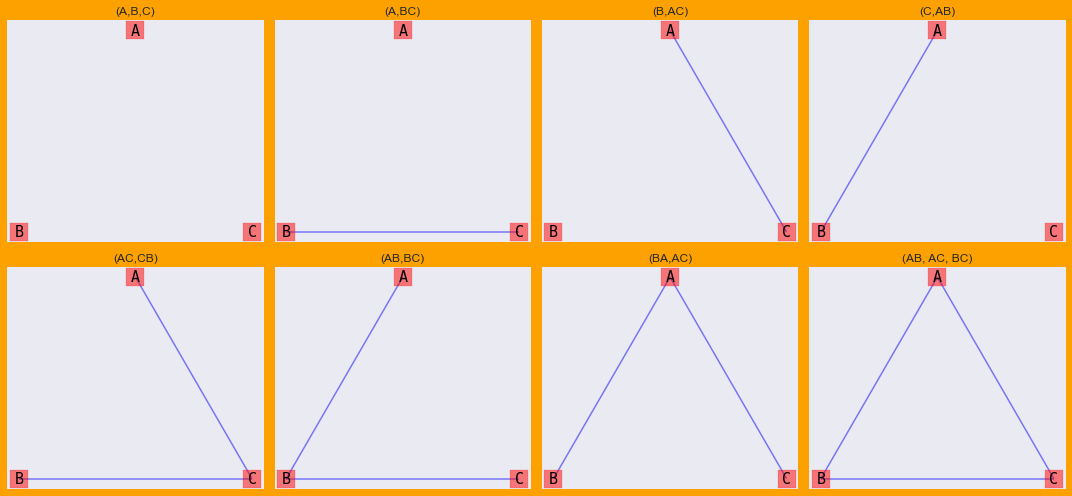
_images/log-linear-graphical_1_0.png

Notice (ABC) was not drawn with the previous graphs/models. That’s because (ABC) is a bit special in its own way in that there is a 3-way interaction between A, B, C. We can draw (ABC) as a factor graph.

[2]:

def draw_abc(ax):
    g = nx.Graph()

    for n in ['A', 'B', 'C', 'ABC']:
        g.add_node(n)

    for u, v in [('A', 'B'), ('B', 'C'), ('A', 'C'), ('A', 'ABC'), ('B', 'ABC'), ('C', 'ABC')]:
        g.add_edge(u, v)

    pos = {
        'A': (200, 250),
        'B': (150, 230),
        'C': (250, 230),
        'ABC': (200, 240)
    }

    params = {
        'nodelist': ['A', 'B', 'C'],
        'node_color': 'r',
        'node_size': 350,
        'node_shape': 's',
        'alpha': 0.5,
        'pos': pos,
        'ax': ax
    }
    _ = nx.drawing.nx_pylab.draw_networkx_nodes(g, **params)

    params = {
        'nodelist': ['ABC'],
        'node_color': 'g',
        'node_size': 450,
        'node_shape': 's',
        'alpha': 0.5,
        'pos': pos,
        'ax': ax
    }
    _ = nx.drawing.nx_pylab.draw_networkx_nodes(g, **params)

    params = {
        'font_size': 15,
        'font_color': 'k',
        'font_family': 'monospace',
        'pos': pos,
        'ax': ax
    }
    _ = nx.drawing.nx_pylab.draw_networkx_labels(g, **params)

    params = {
        'width': 1.5,
        'alpha': 0.5,
        'edge_color': 'b',
        'arrowsize': 20,
        'pos': pos,
        'ax': ax
    }
    _ = nx.drawing.nx_pylab.draw_networkx_edges(g, **params)

    ax.set_title('ABC')
    ax.grid(False)

fig, ax = plt.subplots(figsize=(4, 3))
draw_abc(ax)
plt.tight_layout()
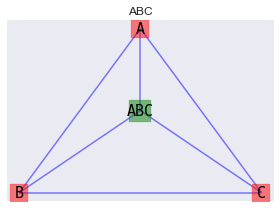
_images/log-linear-graphical_3_0.png

10.1. Bayesian Network, Data

Let’s create a Bayesian Belief Network BBN with three nodes A, B and C and the serial structure A -> B -> C.

[3]:

from pybbn.graph.dag import Bbn
from pybbn.graph.edge import Edge, EdgeType
from pybbn.graph.node import BbnNode
from pybbn.graph.variable import Variable
from pybbn.generator.bbngenerator import convert_for_drawing

a = BbnNode(Variable(0, 'a', ['on', 'off']), [0.5, 0.5])
b = BbnNode(Variable(1, 'b', ['on', 'off']), [0.5, 0.5, 0.4, 0.6])
c = BbnNode(Variable(2, 'c', ['on', 'off']), [0.7, 0.3, 0.2, 0.8])

bbn = Bbn() \
    .add_node(a) \
    .add_node(b) \
    .add_node(c) \
    .add_edge(Edge(a, b, EdgeType.DIRECTED)) \
    .add_edge(Edge(b, c, EdgeType.DIRECTED))

g = convert_for_drawing(bbn)

fig, ax = plt.subplots(figsize=(5, 3))

nx.draw(**{
    'G': g,
    'ax': ax,
    'pos': nx.spiral_layout(g),
    'with_labels': True,
    'labels': {0: 'A', 1: 'B', 2: 'C'},
    'node_color': 'r'
})
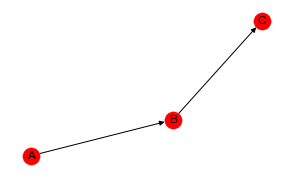
_images/log-linear-graphical_5_0.png

A contigency table may be created from the sampled data of the BBN.

[4]:

import pandas as pd
from pybbn.sampling.sampling import LogicSampler

sampler = LogicSampler(bbn)
df = pd.DataFrame(sampler.get_samples(n_samples=1_000, seed=37)) \
    .rename(columns={0: 'a', 1: 'b', 2: 'c'}) \
    .assign(n=1) \
    .groupby(['a', 'b', 'c']) \
    .agg('sum') \
    .reset_index()

[5]:

df

[5]:
a b c n
0 off off off 238
1 off off on 54
2 off on off 53
3 off on on 127
4 on off off 202
5 on off on 61
6 on on off 82
7 on on on 183

10.2. Likelihood and deviance

Now, let’s specify the LLMs and see which one best explains the data. As you can see, the homogenous model (AB, AC, BC) and the conditional independence model (AB, BC) are comptetitive with one another (they have the lowest deviance and the highest log-likelihood).

[6]:

from patsy import dmatrices
import statsmodels.api as sm

def get_stats(formula, df):
    y, X = dmatrices(formula, df, return_type='dataframe')
    r = sm.GLM(y, X, family=sm.families.Poisson()).fit()

    return {
        'df_model': r.df_model,
        'deviance': r.deviance,
        'log_likelihood': r.llf
    }

formulas = {
    '(A,B,C)': 'n ~ a + b + c',
    '(A,BC)': 'n ~ a + b*c',
    '(B,AC)': 'n ~ b + a*c',
    '(C,AB)': 'n ~ c + a*b',
    '(AC,CB)': 'n ~ a*c + c*b',
    '(AB,BC)': 'n ~ a*b + b*c',
    '(BA,AC)': 'n ~ b*a + a*c',
    '(AB, AC, BC)': 'n ~ (a + b + c)**2'
}

pd.DataFrame([{**{'model': m}, **get_stats(f, df)} for m, f in formulas.items()])

[6]:
model df_model deviance log_likelihood
0 (A,B,C) 3 267.851450 -159.940146
1 (A,BC) 4 16.687786 -34.358314
2 (B,AC) 4 261.530543 -156.779692
3 (C,AB) 4 253.136932 -152.582887
4 (AC,CB) 5 10.366879 -31.197860
5 (AB,BC) 5 1.973268 -27.001055
6 (BA,AC) 5 246.816025 -149.422433
7 (AB, AC, BC) 6 1.445598 -26.737220

10.3. Detecting model differences

We might want to try to some hypothesis testing to see if there is any real differences between these LLMs. Let’s sample 10 different data sets and apply each model over these data sets. We will then compute the averages and apply a 1-way ANOVA test to see if there are any differences in terms of deviance and log-likelhood.

[7]:

result_df = []

for _ in range(10):
    df = pd.DataFrame(sampler.get_samples(n_samples=1_000, seed=37)) \
        .rename(columns={0: 'a', 1: 'b', 2: 'c'}) \
        .assign(n=1) \
        .groupby(['a', 'b', 'c']) \
        .agg('sum') \
        .reset_index()

    r = pd.DataFrame([{**{'model': m}, **get_stats(f, df)} for m, f in formulas.items()])
    result_df.append(r)

result_df = pd.concat(result_df)

[8]:

result_df \
    .groupby(['model']) \
    .agg('mean') \
    .sort_values(['log_likelihood', 'deviance'], ascending=[False, False])

[8]:
df_model deviance log_likelihood
model
(AB, AC, BC) 6 1.445598 -26.737220
(AB,BC) 5 1.973268 -27.001055
(AC,CB) 5 10.366879 -31.197860
(A,BC) 4 16.687786 -34.358314
(BA,AC) 5 246.816025 -149.422433
(C,AB) 4 253.136932 -152.582887
(B,AC) 4 261.530543 -156.779692
(A,B,C) 3 267.851450 -159.940146

10.3.1. Deviance

As you can see, there is statistically significant difference between the deviances using a 1-way ANOVA test.

[9]:

from statsmodels.formula.api import ols

model = ols('deviance ~ model', result_df).fit()
model.summary()

[9]:
OLS Regression Results
Dep. Variable: deviance R-squared: 1.000
Model: OLS Adj. R-squared: 1.000
Method: Least Squares F-statistic: 2.034e+31
Date: Fri, 25 Mar 2022 Prob (F-statistic): 0.00
Time: 17:52:19 Log-Likelihood: 2290.5
No. Observations: 80 AIC: -4565.
Df Residuals: 72 BIC: -4546.
Df Model: 7
Covariance Type: nonrobust
coef std err t P>|t| [0.025 0.975]
Intercept 267.8515 2.96e-14 9.03e+15 0.000 267.851 267.851
model[T.(A,BC)] -251.1637 4.19e-14 -5.99e+15 0.000 -251.164 -251.164
model[T.(AB, AC, BC)] -266.4059 4.19e-14 -6.35e+15 0.000 -266.406 -266.406
model[T.(AB,BC)] -265.8782 4.19e-14 -6.34e+15 0.000 -265.878 -265.878
model[T.(AC,CB)] -257.4846 4.19e-14 -6.14e+15 0.000 -257.485 -257.485
model[T.(B,AC)] -6.3209 4.19e-14 -1.51e+14 0.000 -6.321 -6.321
model[T.(BA,AC)] -21.0354 4.19e-14 -5.02e+14 0.000 -21.035 -21.035
model[T.(C,AB)] -14.7145 4.19e-14 -3.51e+14 0.000 -14.715 -14.715
Omnibus: 16.820 Durbin-Watson: 2.250
Prob(Omnibus): 0.000 Jarque-Bera (JB): 9.494
Skew: -0.676 Prob(JB): 0.00868
Kurtosis: 1.991 Cond. No. 8.89


Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.

Using Tukey’s Honestly Significant Difference HSD test, we can inspect which pairs of models are different. We find that all pairs of models are different with satistical significance.

[10]:

from statsmodels.stats.multicomp import pairwise_tukeyhsd
tukey = pairwise_tukeyhsd(endog=result_df['deviance'], groups=result_df['model'], alpha=0.05)
tukey.summary()

[10]:
Multiple Comparison of Means - Tukey HSD, FWER=0.05
group1 group2 meandiff p-adj lower upper reject
(A,B,C) (A,BC) -251.1637 0.001 -251.1637 -251.1637 True
(A,B,C) (AB, AC, BC) -266.4059 0.001 -266.4059 -266.4059 True
(A,B,C) (AB,BC) -265.8782 0.001 -265.8782 -265.8782 True
(A,B,C) (AC,CB) -257.4846 0.001 -257.4846 -257.4846 True
(A,B,C) (B,AC) -6.3209 0.001 -6.3209 -6.3209 True
(A,B,C) (BA,AC) -21.0354 0.001 -21.0354 -21.0354 True
(A,B,C) (C,AB) -14.7145 0.001 -14.7145 -14.7145 True
(A,BC) (AB, AC, BC) -15.2422 0.001 -15.2422 -15.2422 True
(A,BC) (AB,BC) -14.7145 0.001 -14.7145 -14.7145 True
(A,BC) (AC,CB) -6.3209 0.001 -6.3209 -6.3209 True
(A,BC) (B,AC) 244.8428 0.001 244.8428 244.8428 True
(A,BC) (BA,AC) 230.1282 0.001 230.1282 230.1282 True
(A,BC) (C,AB) 236.4491 0.001 236.4491 236.4491 True
(AB, AC, BC) (AB,BC) 0.5277 0.001 0.5277 0.5277 True
(AB, AC, BC) (AC,CB) 8.9213 0.001 8.9213 8.9213 True
(AB, AC, BC) (B,AC) 260.0849 0.001 260.0849 260.0849 True
(AB, AC, BC) (BA,AC) 245.3704 0.001 245.3704 245.3704 True
(AB, AC, BC) (C,AB) 251.6913 0.001 251.6913 251.6913 True
(AB,BC) (AC,CB) 8.3936 0.001 8.3936 8.3936 True
(AB,BC) (B,AC) 259.5573 0.001 259.5573 259.5573 True
(AB,BC) (BA,AC) 244.8428 0.001 244.8428 244.8428 True
(AB,BC) (C,AB) 251.1637 0.001 251.1637 251.1637 True
(AC,CB) (B,AC) 251.1637 0.001 251.1637 251.1637 True
(AC,CB) (BA,AC) 236.4491 0.001 236.4491 236.4491 True
(AC,CB) (C,AB) 242.7701 0.001 242.7701 242.7701 True
(B,AC) (BA,AC) -14.7145 0.001 -14.7145 -14.7145 True
(B,AC) (C,AB) -8.3936 0.001 -8.3936 -8.3936 True
(BA,AC) (C,AB) 6.3209 0.001 6.3209 6.3209 True

10.3.2. Log-likelihood

Now, we will do the same to see if there’s a difference with the log-likelihood.

[11]:

model = ols('log_likelihood ~ model', result_df).fit()
model.summary()

[11]:
OLS Regression Results
Dep. Variable: log_likelihood R-squared: 1.000
Model: OLS Adj. R-squared: 1.000
Method: Least Squares F-statistic: 1.163e+31
Date: Fri, 25 Mar 2022 Prob (F-statistic): 0.00
Time: 17:52:19 Log-Likelihood: 2323.6
No. Observations: 80 AIC: -4631.
Df Residuals: 72 BIC: -4612.
Df Model: 7
Covariance Type: nonrobust
coef std err t P>|t| [0.025 0.975]
Intercept -159.9401 1.96e-14 -8.16e+15 0.000 -159.940 -159.940
model[T.(A,BC)] 125.5818 2.77e-14 4.53e+15 0.000 125.582 125.582
model[T.(AB, AC, BC)] 133.2029 2.77e-14 4.8e+15 0.000 133.203 133.203
model[T.(AB,BC)] 132.9391 2.77e-14 4.8e+15 0.000 132.939 132.939
model[T.(AC,CB)] 128.7423 2.77e-14 4.64e+15 0.000 128.742 128.742
model[T.(B,AC)] 3.1605 2.77e-14 1.14e+14 0.000 3.160 3.160
model[T.(BA,AC)] 10.5177 2.77e-14 3.79e+14 0.000 10.518 10.518
model[T.(C,AB)] 7.3573 2.77e-14 2.65e+14 0.000 7.357 7.357
Omnibus: 6.312 Durbin-Watson: 1.121
Prob(Omnibus): 0.043 Jarque-Bera (JB): 6.508
Skew: 0.685 Prob(JB): 0.0386
Kurtosis: 2.729 Cond. No. 8.89


Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.

We will use Tukey’s HSD test again.

[12]:

tukey = pairwise_tukeyhsd(endog=result_df['log_likelihood'], groups=result_df['model'], alpha=0.05)
tukey.summary()

[12]:
Multiple Comparison of Means - Tukey HSD, FWER=0.05
group1 group2 meandiff p-adj lower upper reject
(A,B,C) (A,BC) 125.5818 0.001 125.5818 125.5818 True
(A,B,C) (AB, AC, BC) 133.2029 0.001 133.2029 133.2029 True
(A,B,C) (AB,BC) 132.9391 0.001 132.9391 132.9391 True
(A,B,C) (AC,CB) 128.7423 0.001 128.7423 128.7423 True
(A,B,C) (B,AC) 3.1605 0.001 3.1605 3.1605 True
(A,B,C) (BA,AC) 10.5177 0.001 10.5177 10.5177 True
(A,B,C) (C,AB) 7.3573 0.001 7.3573 7.3573 True
(A,BC) (AB, AC, BC) 7.6211 0.001 7.6211 7.6211 True
(A,BC) (AB,BC) 7.3573 0.001 7.3573 7.3573 True
(A,BC) (AC,CB) 3.1605 0.001 3.1605 3.1605 True
(A,BC) (B,AC) -122.4214 0.001 -122.4214 -122.4214 True
(A,BC) (BA,AC) -115.0641 0.001 -115.0641 -115.0641 True
(A,BC) (C,AB) -118.2246 0.001 -118.2246 -118.2246 True
(AB, AC, BC) (AB,BC) -0.2638 0.001 -0.2638 -0.2638 True
(AB, AC, BC) (AC,CB) -4.4606 0.001 -4.4606 -4.4606 True
(AB, AC, BC) (B,AC) -130.0425 0.001 -130.0425 -130.0425 True
(AB, AC, BC) (BA,AC) -122.6852 0.001 -122.6852 -122.6852 True
(AB, AC, BC) (C,AB) -125.8457 0.001 -125.8457 -125.8457 True
(AB,BC) (AC,CB) -4.1968 0.001 -4.1968 -4.1968 True
(AB,BC) (B,AC) -129.7786 0.001 -129.7786 -129.7786 True
(AB,BC) (BA,AC) -122.4214 0.001 -122.4214 -122.4214 True
(AB,BC) (C,AB) -125.5818 0.001 -125.5818 -125.5818 True
(AC,CB) (B,AC) -125.5818 0.001 -125.5818 -125.5818 True
(AC,CB) (BA,AC) -118.2246 0.001 -118.2246 -118.2246 True
(AC,CB) (C,AB) -121.385 0.001 -121.385 -121.385 True
(B,AC) (BA,AC) 7.3573 0.001 7.3573 7.3573 True
(B,AC) (C,AB) 4.1968 0.001 4.1968 4.1968 True
(BA,AC) (C,AB) -3.1605 0.001 -3.1605 -3.1605 True

What’s the point of all these tests? We are trying to find a model that best fits the data using LLMs. It would be very interesting and fruitful if the “best” LLM can help us with the true graphical relationships of the variables. In this notebook, you can see that the homogenous association model and one of the conditional independence models are very competitive in terms of deviance and log-likelhood. The true relationship is known, since the data was sampled from a known BBN structure, and so the conditional independence model should be the optimal LLM representation. But, the homogenous association model “performed” better in terms of deviance and log-likelhood. However, the homogenous association model has better performance at the cost of model complexity (more degrees of freedom).

10.4. Joint independence

In this example, we create a BBN with variables A, B and C where we have only A -> B.

[13]:

a = BbnNode(Variable(0, 'a', ['on', 'off']), [0.5, 0.5])
b = BbnNode(Variable(1, 'b', ['on', 'off']), [0.5, 0.5, 0.4, 0.6])
c = BbnNode(Variable(2, 'c', ['on', 'off']), [0.5, 0.5])

bbn = Bbn() \
    .add_node(a) \
    .add_node(b) \
    .add_node(c) \
    .add_edge(Edge(a, b, EdgeType.DIRECTED))

g = convert_for_drawing(bbn)

fig, ax = plt.subplots(figsize=(5, 3))

nx.draw(**{
    'G': g,
    'ax': ax,
    'pos': nx.spiral_layout(g),
    'with_labels': True,
    'labels': {0: 'A', 1: 'B', 2: 'C'},
    'node_color': 'r'
})
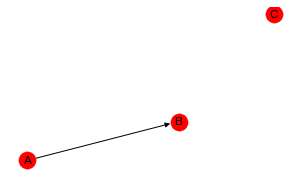
_images/log-linear-graphical_24_0.png

Observe how deviance is always best with the homogenous model. However, the log-likelihood of (C,AB) is very competitive with better performing models.

[14]:

sampler = LogicSampler(bbn)
df = pd.DataFrame(sampler.get_samples(n_samples=1_000, seed=37)) \
    .rename(columns={0: 'a', 1: 'b', 2: 'c'}) \
    .assign(n=1) \
    .groupby(['a', 'b', 'c']) \
    .agg('sum') \
    .reset_index()

result_df = []

for _ in range(10):
    df = pd.DataFrame(sampler.get_samples(n_samples=1_000, seed=37)) \
        .rename(columns={0: 'a', 1: 'b', 2: 'c'}) \
        .assign(n=1) \
        .groupby(['a', 'b', 'c']) \
        .agg('sum') \
        .reset_index()

    r = pd.DataFrame([{**{'model': m}, **get_stats(f, df)} for m, f in formulas.items()])
    result_df.append(r)

result_df = pd.concat(result_df)

result_df \
    .groupby(['model']) \
    .agg('mean') \
    .sort_values(['log_likelihood', 'deviance'], ascending=[False, False])

[14]:
df_model deviance log_likelihood
model
(AB, AC, BC) 6 0.322293 -26.764887
(BA,AC) 5 0.405884 -26.806682
(AB,BC) 5 0.815281 -27.011381
(C,AB) 4 0.857531 -27.032506
(AC,CB) 5 15.078151 -34.142816
(B,AC) 4 15.120402 -34.163942
(A,BC) 4 15.529799 -34.368640
(A,B,C) 3 15.572049 -34.389765

10.5. Complete independence

In this last example, we create a BBN with A, B and C and no edges between them.

[15]:

a = BbnNode(Variable(0, 'a', ['on', 'off']), [0.5, 0.5])
b = BbnNode(Variable(1, 'b', ['on', 'off']), [0.5, 0.5])
c = BbnNode(Variable(2, 'c', ['on', 'off']), [0.5, 0.5])

bbn = Bbn() \
    .add_node(a) \
    .add_node(b) \
    .add_node(c)

g = convert_for_drawing(bbn)

fig, ax = plt.subplots(figsize=(5, 3))

nx.draw(**{
    'G': g,
    'ax': ax,
    'pos': nx.spiral_layout(g),
    'with_labels': True,
    'labels': {0: 'A', 1: 'B', 2: 'C'},
    'node_color': 'r'
})
_images/log-linear-graphical_28_0.png

All the models now seem to be competitive with one another based on the log-likelihood.

[16]:

sampler = LogicSampler(bbn)
df = pd.DataFrame(sampler.get_samples(n_samples=1_000, seed=37)) \
    .rename(columns={0: 'a', 1: 'b', 2: 'c'}) \
    .assign(n=1) \
    .groupby(['a', 'b', 'c']) \
    .agg('sum') \
    .reset_index()

result_df = []

for _ in range(10):
    df = pd.DataFrame(sampler.get_samples(n_samples=1_000, seed=37)) \
        .rename(columns={0: 'a', 1: 'b', 2: 'c'}) \
        .assign(n=1) \
        .groupby(['a', 'b', 'c']) \
        .agg('sum') \
        .reset_index()

    r = pd.DataFrame([{**{'model': m}, **get_stats(f, df)} for m, f in formulas.items()])
    result_df.append(r)

result_df = pd.concat(result_df)

result_df \
    .groupby(['model']) \
    .agg('mean') \
    .sort_values(['log_likelihood', 'deviance'], ascending=[False, False])

[16]:
df_model deviance log_likelihood
model
(AB, AC, BC) 6 0.520471 -26.921138
(AC,CB) 5 0.593338 -26.957571
(BA,AC) 5 0.719971 -27.020888
(B,AC) 4 0.787820 -27.054812
(AB,BC) 5 0.977137 -27.149470
(A,BC) 4 1.044986 -27.183395
(C,AB) 4 1.171619 -27.246712
(A,B,C) 3 1.239468 -27.280636