5. Logistic Regression and Naive Bayes

5.1. Simulate data

from pybbn.graph.dag import Bbn
from pybbn.graph.edge import Edge, EdgeType
from pybbn.graph.jointree import EvidenceBuilder
from pybbn.graph.node import BbnNode
from pybbn.graph.variable import Variable
from pybbn.pptc.inferencecontroller import InferenceController

y = BbnNode(Variable(0, 'y', [0, 1]), [0.9, 0.1])
x1 = BbnNode(Variable(1, 'x1', [0, 1]), [0.9, 0.1, 0.1, 0.9])
x2 = BbnNode(Variable(2, 'x2', [0, 1]), [0.1, 0.9, 0.9, 0.1])

bbn = Bbn() \
    .add_node(y) \
    .add_node(x1) \
    .add_node(x2) \
    .add_edge(Edge(y, x1, EdgeType.DIRECTED)) \
    .add_edge(Edge(y, x2, EdgeType.DIRECTED))

join_tree = InferenceController.apply(bbn)

for node, posteriors in join_tree.get_posteriors().items():
    p = ', '.join([f'{val}={prob:.5f}' for val, prob in posteriors.items()])
    print(f'{node} : {p}')

y : 0=0.90000, 1=0.10000
x1 : 0=0.82000, 1=0.18000
x2 : 0=0.18000, 1=0.82000

from pybbn.sampling.sampling import LogicSampler
import pandas as pd

N = 10_000

sampler = LogicSampler(bbn)
samples = sampler.get_samples(n_samples=N, seed=37)

tr_df = pd.DataFrame(sampler.get_samples(n_samples=N, seed=37)).rename(columns={0: 'y', 1: 'x1', 2: 'x2'})
te_df = pd.DataFrame(sampler.get_samples(n_samples=N, seed=37)).rename(columns={0: 'y', 1: 'x1', 2: 'x2'})

y_tr = tr_df.y
y_te = te_df.y

X_tr = tr_df[['x1', 'x2']]
X_te = te_df[['x1', 'x2']]

5.2. Logistic regression

from sklearn.linear_model import LogisticRegression
from sklearn.metrics import roc_auc_score, average_precision_score

lr = LogisticRegression(solver='saga')
lr.fit(X_tr, y_tr)

print(lr.intercept_)
print(lr.coef_)

y_pred = lr.predict_proba(X_te)[:,1]

print(roc_auc_score(y_te, y_pred))
print(average_precision_score(y_te, y_pred))

[-2.16512394]
[[ 4.15491386 -4.08266375]]
0.969224166856079
0.8021200552659064

from sklearn.metrics import roc_curve, precision_recall_curve
import matplotlib.pyplot as plt
import numpy as np

plt.style.use('ggplot')

def plot_roc(ax, y, y_pred):
    fpr, tpr, _ = roc_curve(y, y_pred)
    score = roc_auc_score(y, y_pred) * 100.0

    ax.step(fpr, tpr, color='b', alpha=0.5, where='post', label='ROC curve')
    ax.plot((0, 1), (0, 1), 'r--', alpha=0.2, label='baseline')
    ax.set_xlabel('fpr')
    ax.set_ylabel('tpr')
    ax.set_title(f'ROC Curve ({score:.1f})')
    ax.legend()

def plot_pr(ax, y, y_pred):
    pre, rec, _ = precision_recall_curve(y, y_pred)
    baseline = np.sum(y) / len(y)
    score = average_precision_score(y, y_pred) * 100.0

    ax.step(rec, pre, color='b', alpha=0.5, where='post', label='PR curve')
    ax.set_xlabel('recall')
    ax.set_ylabel('precision')
    ax.set_title(f'Precision-Recall Curve ({score:.1f})')
    ax.plot((0, 1), (baseline, baseline), 'r--', alpha=0.3, label='baseline')
    ax.legend()

def do_plots(y, y_pred):
    fig, ax = plt.subplots(1, 2, figsize=(15, 5))
    plot_roc(ax[0], y, y_pred)
    plot_pr(ax[1], y, y_pred)

    plt.tight_layout()

do_plots(y_te, y_pred)

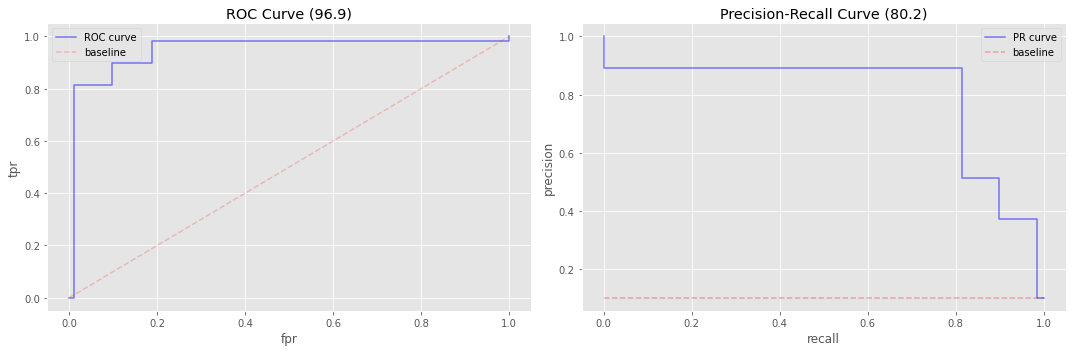
5.3. Random forest

from sklearn.ensemble import RandomForestClassifier

rf = RandomForestClassifier(random_state=37)
rf.fit(X_tr, y_tr)

y_pred = rf.predict_proba(X_te)[:,1]
print(roc_auc_score(y_te, y_pred))
print(average_precision_score(y_te, y_pred))
do_plots(y_te, y_pred)

0.969224166856079
0.8021200552659064

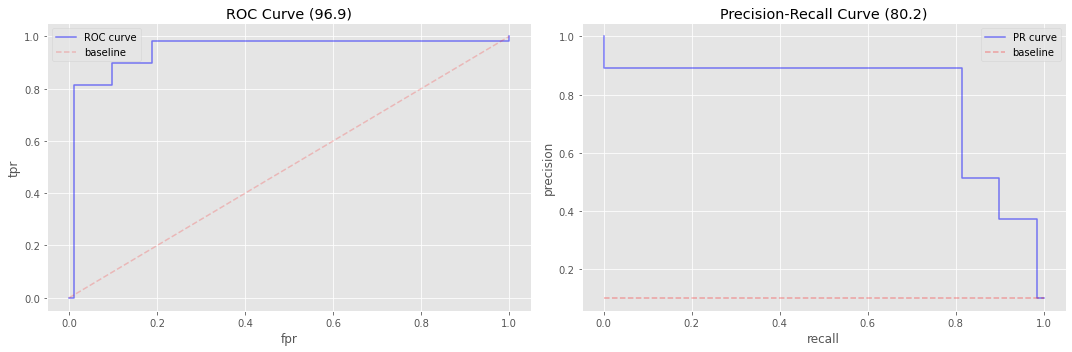
5.4. Gaussian Naive Bayes

from sklearn.naive_bayes import GaussianNB

nb = GaussianNB()
nb.fit(X_tr, y_tr)

y_pred = nb.predict_proba(X_te)[:,1]

print(roc_auc_score(y_te, y_pred))
print(average_precision_score(y_te, y_pred))
do_plots(y_te, y_pred)

0.969224166856079
0.8021200552659064

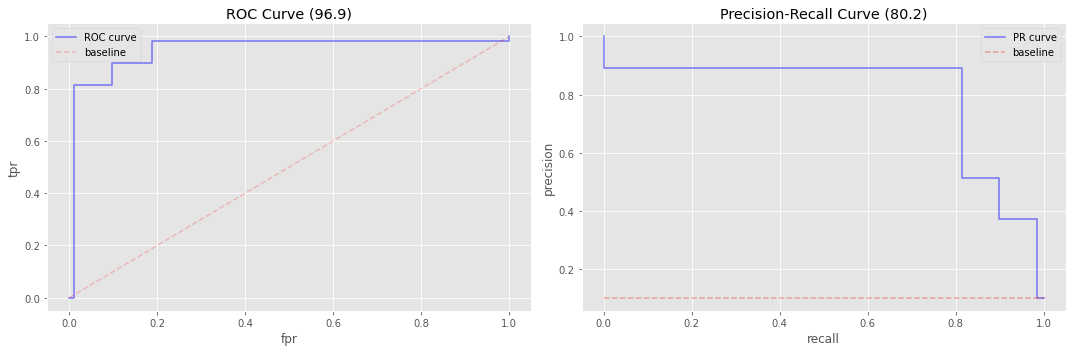
5.5. Support Vector Machine

from sklearn.svm import NuSVC

svm = NuSVC(nu=0.1, kernel='linear', probability=True, random_state=37)
svm.fit(X_tr, y_tr)

y_pred = svm.predict_proba(X_te)[:,1]

print(roc_auc_score(y_te, y_pred))
print(average_precision_score(y_te, y_pred))
do_plots(y_te, y_pred)

0.9686717320951175
0.8007435038526662

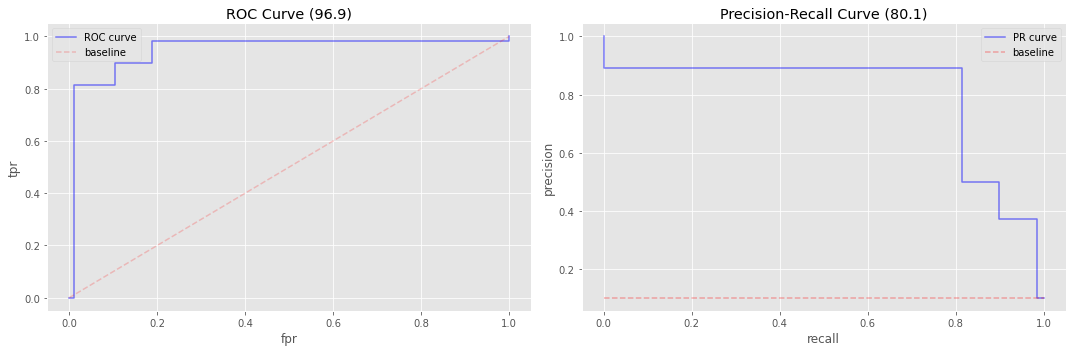
5.6. Bayesian Belief Network

5.6.1. \(X_1 \leftarrow Y \rightarrow X_2\)

import pandas as pd

df = tr_df

y_0 = df[df.y == 0].shape[0] / df.shape[0]
y_1 = df[df.y == 1].shape[0] / df.shape[0]

x1_00 = df[(df.y == 0) & (df.x1 == 0)].shape[0] / df.shape[0] / y_0
x1_01 = df[(df.y == 0) & (df.x1 == 1)].shape[0] / df.shape[0] / y_0
x1_10 = df[(df.y == 1) & (df.x1 == 0)].shape[0] / df.shape[0] / y_1
x1_11 = df[(df.y == 1) & (df.x1 == 1)].shape[0] / df.shape[0] / y_1

x2_00 = df[(df.y == 0) & (df.x2 == 0)].shape[0] / df.shape[0] / y_0
x2_01 = df[(df.y == 0) & (df.x2 == 1)].shape[0] / df.shape[0] / y_0
x2_10 = df[(df.y == 1) & (df.x2 == 0)].shape[0] / df.shape[0] / y_1
x2_11 = df[(df.y == 1) & (df.x2 == 1)].shape[0] / df.shape[0] / y_1

print(y_0, y_1)
print(x1_00, x1_01, x1_10, x1_11)
print(x2_00, x2_01, x2_10, x2_11)

0.897 0.103
0.9028985507246376 0.09710144927536231 0.10097087378640776 0.8990291262135923
0.1035674470457079 0.8964325529542921 0.8990291262135923 0.10097087378640776

y = BbnNode(Variable(0, 'y', ['off', 'on']), [y_0, y_1])
x1 = BbnNode(Variable(1, 'x1', ['off', 'on']), [x1_00, x1_01, x1_10, x1_11])
x2 = BbnNode(Variable(2, 'x2', ['off', 'on']), [x2_00, x2_01, x2_10, x2_11])

bbn = Bbn() \
    .add_node(y) \
    .add_node(x1) \
    .add_node(x2) \
    .add_edge(Edge(y, x1, EdgeType.DIRECTED)) \
    .add_edge(Edge(y, x2, EdgeType.DIRECTED))

join_tree = InferenceController.apply(bbn)

for node, posteriors in join_tree.get_posteriors().items():
    p = ', '.join([f'{val}={prob:.5f}' for val, prob in posteriors.items()])
    print(f'{node} : {p}')

y : off=0.89700, on=0.10300
x1 : off=0.82030, on=0.17970
x2 : off=0.18550, on=0.81450

def predict_proba(r):
    x1_val = 'off' if r.x1 == 0 else 'on'
    x2_val = 'off' if r.x2 == 0 else 'on'

    ev1 = EvidenceBuilder() \
            .with_node(join_tree.get_bbn_node_by_name('x1')) \
            .with_evidence(x1_val, 1.0) \
            .build()
    ev2 = EvidenceBuilder() \
            .with_node(join_tree.get_bbn_node_by_name('x2')) \
            .with_evidence(x2_val, 1.0) \
            .build()
    ev = [ev1, ev2]

    join_tree.unobserve_all()
    join_tree.update_evidences(ev)
    posteriors = join_tree.get_posteriors()
    score = posteriors['y']['on']

    return score

y_pred = [predict_proba(r) for _, r in te_df.iterrows()]

print(roc_auc_score(y_te, y_pred))
print(average_precision_score(y_te, y_pred))
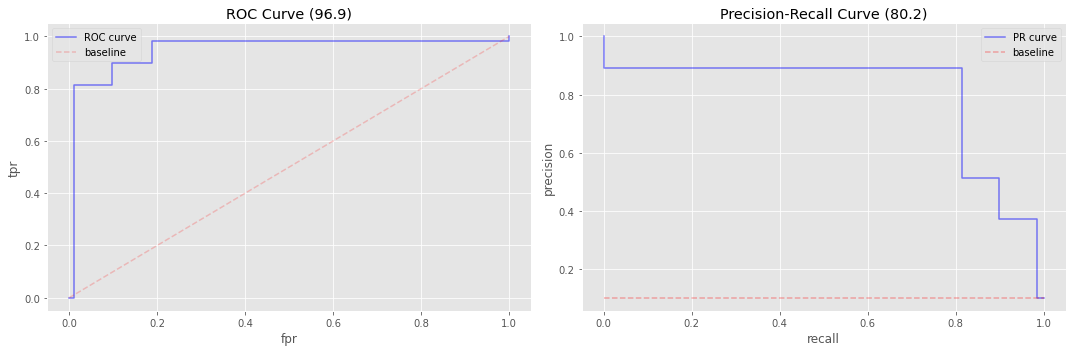
do_plots(y_te, y_pred)

0.969224166856079
0.8021200552659064

5.6.2. \(X_1 \rightarrow Y \leftarrow X_2\)

x1_0 = df[df.x1 == 0].shape[0] / df.shape[0]
x1_1 = df[df.x1 == 1].shape[0] / df.shape[0]

x2_0 = df[df.x2 == 0].shape[0] / df.shape[0]
x2_1 = df[df.x2 == 1].shape[0] / df.shape[0]


y_000 = (df[(df.x1 == 0) & (df.x2 == 0) & (df.y == 0)].shape[0] / df.shape[0]) / (df[(df.x1 == 0) & (df.x2 == 0)].shape[0] / df.shape[0])
y_001 = (df[(df.x1 == 0) & (df.x2 == 0) & (df.y == 1)].shape[0] / df.shape[0]) / (df[(df.x1 == 0) & (df.x2 == 0)].shape[0] / df.shape[0])
y_010 = (df[(df.x1 == 0) & (df.x2 == 1) & (df.y == 0)].shape[0] / df.shape[0]) / (df[(df.x1 == 0) & (df.x2 == 1)].shape[0] / df.shape[0])
y_011 = (df[(df.x1 == 0) & (df.x2 == 1) & (df.y == 1)].shape[0] / df.shape[0]) / (df[(df.x1 == 0) & (df.x2 == 1)].shape[0] / df.shape[0])
y_100 = (df[(df.x1 == 1) & (df.x2 == 0) & (df.y == 0)].shape[0] / df.shape[0]) / (df[(df.x1 == 1) & (df.x2 == 0)].shape[0] / df.shape[0])
y_101 = (df[(df.x1 == 1) & (df.x2 == 0) & (df.y == 1)].shape[0] / df.shape[0]) / (df[(df.x1 == 1) & (df.x2 == 0)].shape[0] / df.shape[0])
y_110 = (df[(df.x1 == 1) & (df.x2 == 1) & (df.y == 0)].shape[0] / df.shape[0]) / (df[(df.x1 == 1) & (df.x2 == 1)].shape[0] / df.shape[0])
y_111 = (df[(df.x1 == 1) & (df.x2 == 1) & (df.y == 1)].shape[0] / df.shape[0]) / (df[(df.x1 == 1) & (df.x2 == 1)].shape[0] / df.shape[0])

print(x1_0, x1_1)
print(x2_0, x2_1)
print(y_000, y_001, y_010, y_011, y_100, y_101, y_110, y_111)

0.8203 0.1797
0.1855 0.8145
0.9037199124726478 0.09628008752735231 0.9978049115104952 0.002195088489504733 0.10945802337938364 0.8905419766206163 0.897196261682243 0.10280373831775702

y = BbnNode(Variable(0, 'y', ['off', 'on']), [y_000, y_001, y_010, y_011, y_100, y_101, y_110, y_111])
x1 = BbnNode(Variable(1, 'x1', ['off', 'on']), [x1_0, x1_1])
x2 = BbnNode(Variable(2, 'x2', ['off', 'on']), [x2_0, x2_1])

bbn = Bbn() \
    .add_node(y) \
    .add_node(x1) \
    .add_node(x2) \
    .add_edge(Edge(x1, y, EdgeType.DIRECTED)) \
    .add_edge(Edge(x2, y, EdgeType.DIRECTED))

join_tree = InferenceController.apply(bbn)

for node, posteriors in join_tree.get_posteriors().items():
    p = ', '.join([f'{val}={prob:.5f}' for val, prob in posteriors.items()])
    print(f'{node} : {p}')

x1 : off=0.82030, on=0.17970
x2 : off=0.18550, on=0.81450
y : off=0.93915, on=0.06085

y_pred = [predict_proba(r) for _, r in te_df.iterrows()]

print(roc_auc_score(y_te, y_pred))
print(average_precision_score(y_te, y_pred))
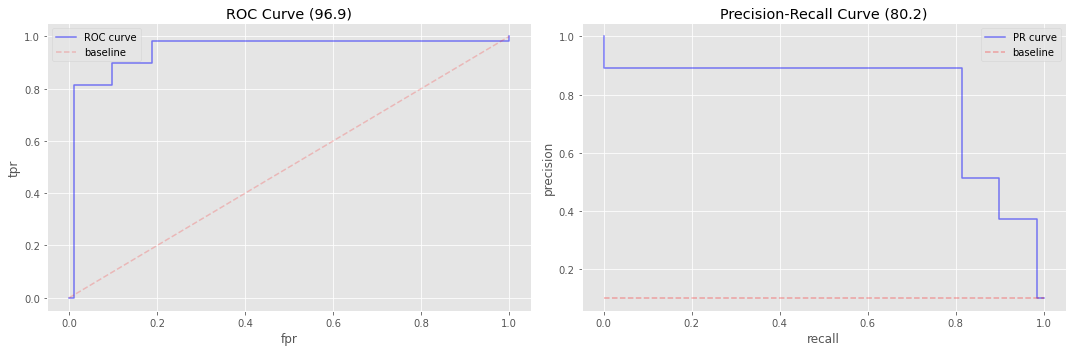
do_plots(y_te, y_pred)

0.969224166856079
0.8021200552659064