4. Optimizing Marginal Revenue from the Demand Curve, Kaggle

Let’s have fun and model profit optimization using the demand curve. The data is take from Kaggle.

4.1. Load data

Let’s load the data.

[1]:

import pandas as pd
import numpy as np

df = pd.read_csv('./data/retail_price.csv') \
    .assign(
        month_year=lambda d: pd.to_datetime(d['month_year']),
        year=lambda d: d['month_year'].dt.year,
        month=lambda d: d['month_year'].dt.month,
        weekend=lambda d: d['weekday'].apply(lambda x: 1 if x >= 5 else 0),
        text=lambda d: d['product_category_name'].apply(lambda s: ' '.join(s.split('_')))
    )
df.shape

[1]:

(676, 31)

4.2. Product categories

There are 9 product categories. Let’s model 9 demand curves corresponding to each of these product categories.

[2]:

df.rename(columns={'product_category_name': 'category'}) \
    .groupby(['category', 'unit_price']) \
    .size() \
    .reset_index() \
    .groupby(['category']) \
    .size()

[2]:

category
bed_bath_table           26
computers_accessories    48
consoles_games           10
cool_stuff               18
furniture_decor          13
garden_tools             56
health_beauty            33
perfumery                14
watches_gifts            78
dtype: int64

4.3. Demand curves by category and price

Here, we shape the data by grouping records into product category and price.

[3]:

pq_df = df.groupby(['product_category_name', 'unit_price']) \
    .agg(
        q=pd.NamedAgg('qty', 'sum')
    ) \
    .reset_index() \
    .rename(columns={'unit_price': 'p', 'product_category_name': 'category'}) \
    .set_index(['category']) \
    .join(df \
        .rename(columns={'product_category_name': 'category'}) \
        .groupby(['category']) \
        .agg(c=pd.NamedAgg('freight_price', 'mean'))
    )
pq_df.shape

[3]:

(296, 3)

4.4. Optimal prices

The table below shows the optimal price for each product category.

[4]:

from sklearn.linear_model import LinearRegression

def get_mc(category):
    return pq_df[pq_df.index==category].iloc[0].c

def get_Xy(category):
    Xy = pq_df[pq_df.index==category]
    X = Xy[['p']]
    y = Xy['q']

    return X, y

def get_model(X, y):
    m = LinearRegression()
    m.fit(X, y)

    return m

def debug_params(model, mc):
    b_0, b_1 = model.intercept_, model.coef_[0]
    qp_params = f'{b_0:.5f} + {b_1:.5f}p'

    z_0, z_1 = (-b_0 / b_1), (1 / b_1)
    pq_params = f'{z_0:.5f} + {z_1:.5f}q'
    tr_params = f'{z_0:.5f}q + {z_1:.5f}q^2'

    z_0, z_1 = (-b_0 / b_1), 2 * (1 / b_1)
    mr_params = f'{z_0:.5f} + {z_1:.5f}q'

    z_0, z_1 = (-b_0 / b_1), 2 * (1 / b_1)
    qo_params = f'({mc:.5f} - {z_0:.5f}) / {z_1:.5f}'

    return {
        'q': qp_params,
        'p': pq_params,
        'tr': tr_params,
        'mr': mr_params,
        'qo': qo_params
    }

def get_params(model):
    return pd.Series([model.intercept_, model.coef_[0]], ['b_0', 'b_1'])

def get_pq(b_0, b_1):
    return lambda q: (-b_0 / b_1) + (1 / b_1) * q

def get_qp(b_0, b_1):
    return lambda p: b_0 + (b_1 * p)

def get_mr(b_0, b_1):
    return lambda q: (-b_0 / b_1) + (2 * (1 / b_1) * q)

def get_qo(b_0, b_1):
    z_0 = (-b_0 / b_1)
    z_1 = 2 * (1 / b_1)
    return lambda mc: (mc - z_0) / z_1

def get_funcs(b_0, b_1):
    pq = get_pq(b_0, b_1)
    qp = get_qp(b_0, b_1)
    mr = get_mr(b_0, b_1)
    qo = get_qo(b_0, b_1)
    r = lambda p, q: p * q
    t = lambda p, q, mc: (p * q) - (mc * q)

    return pq, qp, mr, qo, r, t

def get_opt(f, mc):
    pq_f, qp_f, mr_f, qo_f, r_f, t_f = f

    q_opt = qo_f(mc)
    p_opt = pq_f(q_opt)
    mr_opt = mr_f(q_opt)
    r_opt = r_f(p_opt, q_opt)
    t_opt = t_f(p_opt, q_opt, mc)

    return pd.Series({
        'mc': mc,
        'p': p_opt,
        'q': q_opt,
        'mr': mr_opt,
        'tr': r_opt,
        'pr': t_opt
    })

def optimize(category):
    X, y = get_Xy(category)
    m = get_model(X, y)
    p = get_params(m)
    f = get_funcs(p.b_0, p.b_1)
    mc = get_mc(category)

    return {**{'category': category}, **get_opt(f, mc).to_dict()}

The category computer_acessories is the outlier here with an optimal price recommended to be a negative price. We will see later that there is an outlier that causes this problem. The columns of the table below are as follows.

mc is marginal cost computed by taking the average cost (average freight cost of all the product items for the particular product catgeory and price point)
p is the optimal price
q is the corresponding optimal quantity
mr is the corresponding marginal revenue
tr is the corresponding total revenue
pr is the corresponding profit

[5]:

opt_df = pd.DataFrame([optimize(c) for c in pq_df.index.unique()])
opt_df

[5]:

	category	mc	p	q	mr	tr	pr
0	bed_bath_table	16.139718	413.954170	21.954253	16.139718	9088.054630	8733.719184
1	computers_accessories	25.103741	-27.221815	6.479547	25.103741	-176.385023	-339.045890
2	consoles_games	14.809415	26.068586	30.257496	14.809415	788.770143	340.674335
3	cool_stuff	18.975096	151.269261	24.424237	18.975096	3694.636306	3231.184067
4	furniture_decor	16.944617	222.175809	38.990538	16.944617	8662.754232	8002.074509
5	garden_tools	28.458310	99.268009	36.931818	28.458310	3666.148045	2615.130919
6	health_beauty	18.607448	849.975469	29.792779	18.607448	25323.131451	24768.763874
7	perfumery	14.336311	78.183209	30.772484	14.336311	2405.891570	1964.727677
8	watches_gifts	16.492840	159.459065	21.486980	16.492840	3426.293739	3071.912418

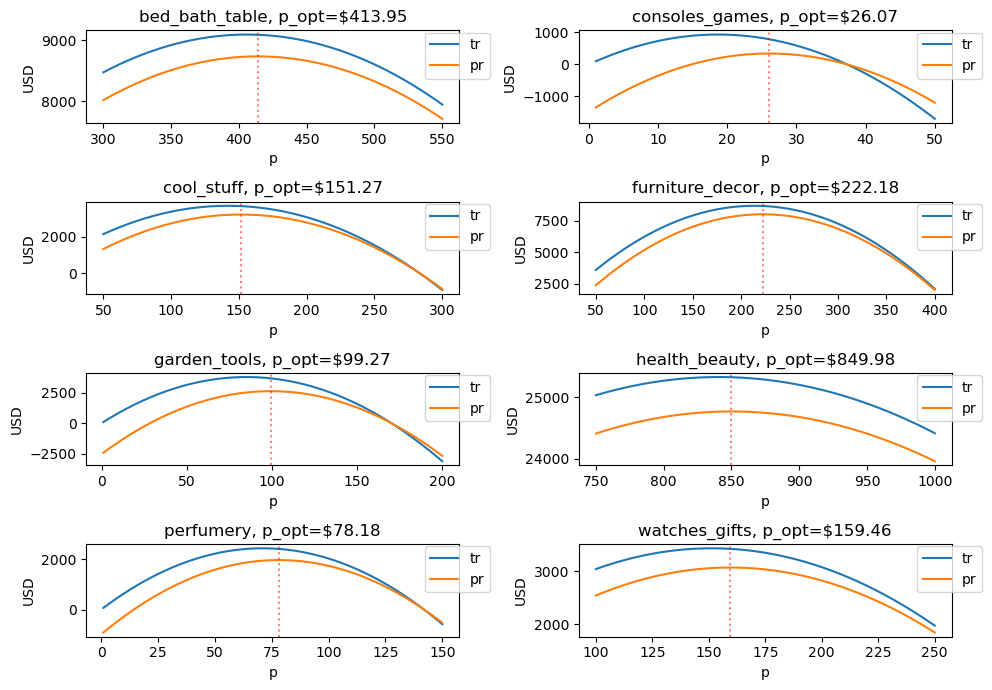
4.5. Visualizing optimal prices

Let’s visualize the total revenue and profit for each product category.

[6]:

import matplotlib.pyplot as plt

def plot_rev_profit_curves(category, min_p=1, max_p=800, ax=None):
    X, y = get_Xy(category)
    m = get_model(X, y)
    p = get_params(m)
    f = get_funcs(p.b_0, p.b_1)
    mc = get_mc(category)
    opt = get_opt(f, mc)

    if ax is None:
        fig, ax = plt.subplots(figsize=(7, 3))
    else:
        fig = None

    pd.DataFrame({
        'p': np.arange(min_p, max_p + 1, 1),

    }).assign(
        q=lambda d: f[1](d['p']),
        tr=lambda d: d['p'] * d['q'],
        mr=lambda d: f[2](d['q']),
        pr=lambda d: f[5](d['p'], d['q'], mc)
    ) \
    .set_index(['p'])[['tr', 'pr']] \
    .plot(kind='line', ax=ax)

    ax.axvline(x=opt.p, color='r', alpha=0.5, linestyle='dotted')
    ax.legend(bbox_to_anchor=(1.1, 1.05))
    ax.set_title(f'{category}, p_opt=${opt.p:.2f}')
    ax.set_ylabel('USD')

    if fig is not None:
        fig.tight_layout()

[7]:

fig, axes = plt.subplots(4, 2, figsize=(10, 7))

categories = [
    'bed_bath_table', 'consoles_games', 'cool_stuff', 'furniture_decor',
    'garden_tools', 'health_beauty', 'perfumery', 'watches_gifts'
]
min_p = [
    300, 1, 50, 50,
    1, 750, 1, 100
]
max_p = [
    550, 50, 300, 400,
    200, 1_000, 150, 250
]

for c, _min_p, _max_p, ax in zip(categories, min_p, max_p, np.ravel(axes)):
    plot_rev_profit_curves(c, min_p=_min_p, max_p=_max_p, ax=ax)

fig.tight_layout()

_images/optimizing-demand-curve-kaggle_13_0.png

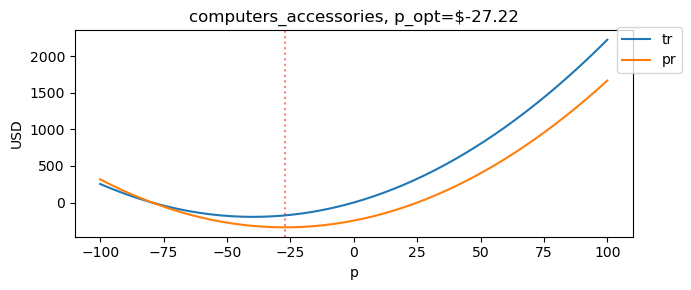
4.6. Computer accessories

Now, what’s wrong with the computers_accesories category? Notice that its total revenue and profit curves are convex (and not concave).

[8]:

plot_rev_profit_curves('computers_accessories', min_p=-100, max_p=100)

_images/optimizing-demand-curve-kaggle_15_0.png

Let’s dig a big deeper.

[9]:

category = 'computers_accessories'
X, y = get_Xy(category)
m = get_model(X, y)
p = get_params(m)
f = get_funcs(p.b_0, p.b_1)
mc = get_mc(category)
opt = get_opt(f, mc)

[10]:

opt

[10]:

mc     25.103741
p     -27.221815
q       6.479547
mr     25.103741
tr   -176.385023
pr   -339.045890
dtype: float64

Look at the relationships below. You will notice that the slopes of q and p are NOT negative but positive (that explains the convex curves).

[11]:

debug_params(m, mc)

[11]:

{'q': '9.85046 + 0.12383p',
 'p': '-79.54737 + 8.07550q',
 'tr': '-79.54737q + 8.07550q^2',
 'mr': '-79.54737 + 16.15099q',
 'qo': '(25.10374 - -79.54737) / 16.15099'}

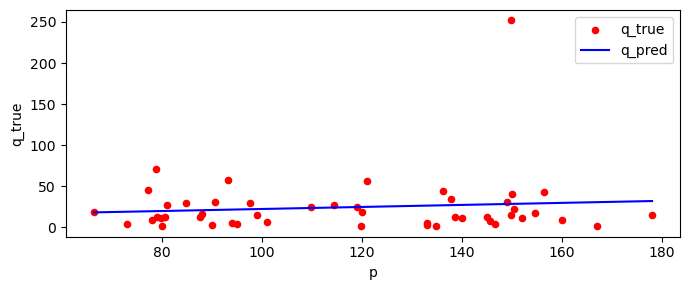
If we visually inspect the data (red dots are scatter plot of true quantity), we notice an outlier quantity around 250. The predicted curve from this data slopes up (positive slope, blue line).

[12]:

fig, ax = plt.subplots(figsize=(7, 3))

_temp = pq_df[pq_df.index==category] \
    .assign(
        q_true=lambda d: d['q'],
        q_pred=lambda d: f[1](d['p'])
    )[['p', 'q_true', 'q_pred']]

_temp.plot(kind='scatter', x='p', y='q_true', label='q_true', ax=ax, color='r')
_temp.plot(kind='line', x='p', y='q_pred', label='q_pred', ax=ax, color='b')

fig.tight_layout()

/opt/anaconda3/lib/python3.9/site-packages/pandas/plotting/_matplotlib/core.py:1114: UserWarning: No data for colormapping provided via 'c'. Parameters 'cmap' will be ignored
  scatter = ax.scatter(

_images/optimizing-demand-curve-kaggle_22_1.png

4.7. Remove outlier

Let’s simply remove the outlier and see what happens.

[13]:

Xy = pq_df[pq_df.index==category].query('q < 252')
X = Xy[['p']]
y = Xy['q']

m = get_model(X, y)
p = get_params(m)
f = get_funcs(p.b_0, p.b_1)
mc = get_mc(category)
opt = get_opt(f, mc)

[14]:

opt

[14]:

mc      25.103741
p      280.092646
q       11.847662
mr      25.103741
tr    3318.442913
pr    3021.022281
dtype: float64

The relationships look better (slopes are negative).

[15]:

debug_params(m, mc)

[15]:

{'q': '24.86173 + -0.04646p',
 'p': '535.08155 + -21.52230q',
 'tr': '535.08155q + -21.52230q^2',
 'mr': '535.08155 + -43.04460q',
 'qo': '(25.10374 - 535.08155) / -43.04460'}

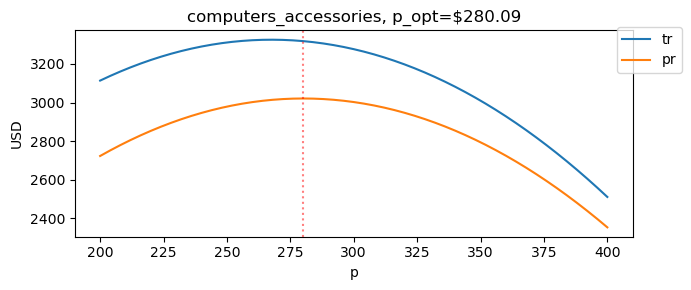
The total revenue and profit curves are now concave.

[16]:

min_p, max_p = 200, 400

fig, ax = plt.subplots(figsize=(7, 3))

pd.DataFrame({
    'p': np.arange(min_p, max_p + 1, 1),

}).assign(
    q=lambda d: f[1](d['p']),
    tr=lambda d: d['p'] * d['q'],
    mr=lambda d: f[2](d['q']),
    pr=lambda d: f[5](d['p'], d['q'], mc)
) \
.set_index(['p'])[['tr', 'pr']] \
.plot(kind='line', ax=ax)

ax.axvline(x=opt.p, color='r', alpha=0.5, linestyle='dotted')
ax.legend(bbox_to_anchor=(1.1, 1.05))
ax.set_title(f'{category}, p_opt=${opt.p:.2f}')
ax.set_ylabel('USD')

fig.tight_layout()

_images/optimizing-demand-curve-kaggle_29_0.png