4. Dimension Reduction or Concept Learning?

It is a common preprocessing step in machine learning goals (eg classification, regression, clustering, etc.) to reduce the dimensionality of the data. Having high dimensionality could lead to different problems for different machine learning tasks. For example, in clustering, high dimensionality might lead to the curse of dimensionality. There is a multitude of approaches for reducing the dimensions of a dataset; these techniques often project the data in the original high-dimensional space to a new lower-dimensional space. The key word here is space; the original high-dimensional space is the raw space where the data exists; the new low-dimensional space is a new space which the data is being projected into.

But what’s the meaning of the new space? The new lower-dimensional space can be interpreted in many different but related ways. One interpretation is that although the new space has a lower number of dimensions, this new space organizes the original dimensions into higher-order meaning. That’s the confusion; the new lower-dimesional space represents higher order meaning. This new space is also called the hidden space or latent space. When dimesion reduction techniques are used, it is better to understand them as a reprojection of the data into a space of higher order meaning, although the new space will have a smaller number of dimensions. These new dimensions are often called components when using techniques like principal component analysis PCA.

Here’s a motivating example. Imagine we have news articles with a lot of words. The representation of these documents could be a vector space model VSM where the documents correspond to rows and words correspond to columns. Each element in the VSM could simply be the count of number of times a word appears in a document. We can project this VSM into a new space where the axes (columns/fields) are higher-order meaning or concepts. For example, the words could be reprojected to their types (eg adjective, verbs, nouns, etc).

In the example below, we will play around with the breast cancer data from Scikit-Learn and apply a few different “dimension reduction” techniques. Let’s see if these techniques can recover any concepts or higher-order meaning from the raw features.

4.1. Breast cancer data

There’s nothing important here; we simply load the data. Note that this dataset is intended for a classification problem. Interesting, 0 denotes malignant and 1 denotes benign. There’s 30 features in this dataset.

from sklearn.datasets import load_breast_cancer

X, y = load_breast_cancer(return_X_y=True, as_frame=True)
y_map = {0: 'malignant', 1: 'benign'}

X.shape, y.shape

((569, 30), (569,))

X.head()

	mean radius	mean texture	mean perimeter	mean area	mean smoothness	mean compactness	mean concavity	mean concave points	mean symmetry	mean fractal dimension	...	worst radius	worst texture	worst perimeter	worst area	worst smoothness	worst compactness	worst concavity	worst concave points	worst symmetry	worst fractal dimension
0	17.99	10.38	122.80	1001.0	0.11840	0.27760	0.3001	0.14710	0.2419	0.07871	...	25.38	17.33	184.60	2019.0	0.1622	0.6656	0.7119	0.2654	0.4601	0.11890
1	20.57	17.77	132.90	1326.0	0.08474	0.07864	0.0869	0.07017	0.1812	0.05667	...	24.99	23.41	158.80	1956.0	0.1238	0.1866	0.2416	0.1860	0.2750	0.08902
2	19.69	21.25	130.00	1203.0	0.10960	0.15990	0.1974	0.12790	0.2069	0.05999	...	23.57	25.53	152.50	1709.0	0.1444	0.4245	0.4504	0.2430	0.3613	0.08758
3	11.42	20.38	77.58	386.1	0.14250	0.28390	0.2414	0.10520	0.2597	0.09744	...	14.91	26.50	98.87	567.7	0.2098	0.8663	0.6869	0.2575	0.6638	0.17300
4	20.29	14.34	135.10	1297.0	0.10030	0.13280	0.1980	0.10430	0.1809	0.05883	...	22.54	16.67	152.20	1575.0	0.1374	0.2050	0.4000	0.1625	0.2364	0.07678

5 rows × 30 columns

y.value_counts().sort_index()

target
0    212
1    357
Name: count, dtype: int64

4.2. Decomposition

We will use 4 different dimension reduction algorithms.

• PCA denoted as pca

• kernel PCA denoted as kpca

• factor analysis denoted as fa

• tSNE denoted as tsne

In the code below,

• M stores the models, and

• D stores the projected data corresponding to the models.

Note that the number of components is hard-coded to 2 for illustration purposes. Ideally, we would want to tune this hyperparameter.

import pandas as pd
import numpy as np
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import StandardScaler
from sklearn.decomposition import PCA, KernelPCA, FactorAnalysis
from sklearn.manifold import TSNE

M = {
    'pca': Pipeline([
        ('scaler', StandardScaler()),
        ('decomposer', PCA(n_components=2, random_state=37))
    ]),
    'kpca': Pipeline([
        ('scaler', StandardScaler()),
        ('decomposer', KernelPCA(n_components=2, kernel='rbf', random_state=37))
    ]),
    'fa': Pipeline([
        ('scaler', StandardScaler()),
        ('decomposer', FactorAnalysis(n_components=2, random_state=37))
    ]),
    'tsne': Pipeline([
        ('scaler', StandardScaler()),
        ('decomposer', TSNE(n_components=2, n_jobs=-1, random_state=37))
    ])
}

to_df = lambda mat: pd.DataFrame(mat, columns=[f'C{i}' for i in range(mat.shape[1])])
D = {k: to_df(m.fit_transform(X)) for k, m in M.items()}

4.3. Density plots

Here are the density plots for the first C0 and second C1 components for each technique.

import matplotlib.pyplot as plt
import seaborn as sns

fig, axes = plt.subplots(1, 4, figsize=(15, 2.5))

for algo, ax, color in zip(D, np.ravel(axes), sns.color_palette('tab10')):
    D[algo]['C0'].plot(kind='kde', ax=ax, title=f'{algo}, C0', color=color)

fig.tight_layout()

fig, axes = plt.subplots(1, 4, figsize=(15, 2.5))

for algo, ax, color in zip(D, np.ravel(axes), sns.color_palette('tab10')):
    D[algo]['C1'].plot(kind='kde', ax=ax, title=f'{algo}, C1', color=color)

fig.tight_layout()

Here are some bivariate density plots for the two components learned by each of the algorithms. PCA and kernel PCA seem to have 2 centers; factor analysis has one and tSNE seem to have 4.

fig, axes = plt.subplots(1, 4, figsize=(15, 2.5))

for algo, ax, color in zip(D, np.ravel(axes), sns.color_palette('tab10')):
    sns.kdeplot(data=D[algo], x='C0', y='C1', ax=ax, color=color)
    ax.set_title(algo)

fig.tight_layout()

4.4. Scatter plots

Take a look at the reprojected data color-coded by class (malignant vs benign). Interestingly, going from 30 dimensions to 2, there seems to be linear separability for all techniques!

import seaborn as sns

def scatter_plot(d, k, ax):
    df = d.assign(y=y)

    for y_val, color in zip(y.unique(), sns.color_palette('tab10')):
        label = y_map[y_val]
        df[df['y']==y_val].plot(
            kind='scatter',
            x='C0',
            y='C1',
            ax=ax,
            color=color,
            label=label,
            s=2
        )

    ax.set_title(k)
    ax.legend(loc='center left', bbox_to_anchor=(1, 0.5))

fig, axes = plt.subplots(2, 2, figsize=(10, 5))

for k, ax in zip(D.keys(), np.ravel(axes)):
    scatter_plot(D[k], k, ax)

fig.tight_layout()

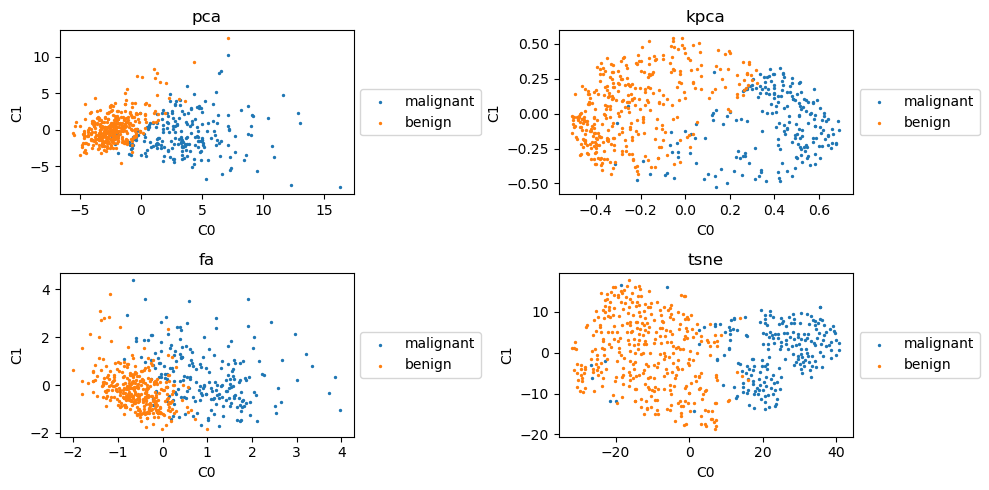
4.5. Classification

If the new dimensions are meaningful, they should help with classification. Below are the non-validated classification performances of each technique. Evidently, PCA and tSNE have the best performances in terms of area under the ROC curve and average precision score.

from sklearn.linear_model import LogisticRegression
from sklearn.metrics import roc_auc_score, average_precision_score

def get_performance(Z, algo):
    m = LogisticRegression(random_state=37, n_jobs=-1, solver='saga', max_iter=10_000)
    m.fit(Z, y)
    y_pred = m.predict(Z)

    roc, aps = roc_auc_score(y, y_pred), average_precision_score(y, y_pred)
    return {
        'algo': algo,
        'roc': roc,
        'aps': aps
    }

pd.DataFrame([get_performance(D[algo], algo) for algo in D.keys()])

	algo	roc	aps
0	pca	0.950617	0.949288
1	kpca	0.922903	0.923345
2	fa	0.910153	0.909794
3	tsne	0.954376	0.952908

Here’s the kicker, learning a logistic regression classification model from the raw dimensions performs worse than learning one using the new and fewer dimensions.

m = LogisticRegression(random_state=37, n_jobs=-1, solver='saga', max_iter=10_000)
m.fit(X, y)
y_pred = m.predict(X)

roc_auc_score(y, y_pred), average_precision_score(y, y_pred)

(0.9086795095396649, 0.9067761384577263)

4.6. Coefficients

If we wanted to know how the old dimensions influences the new ones, we can perform regression. Since there are 2 components, we will compute 2 regressions of the component on the old dimensions for each algorithm. Below, after we get the regression coefficients, we rescale them to the range [20, 100] to make side-by-side comparison of the coefficients easier.

from sklearn.linear_model import LinearRegression, Lasso, Ridge, ElasticNet
from sklearn.ensemble import RandomForestRegressor
from sklearn.preprocessing import MinMaxScaler

def get_components(algo, regressor='rf'):
    def get_regressor():
        regressors = {
            'linear': lambda: LinearRegression(fit_intercept=False, n_jobs=-1),
            'ridge': lambda: Ridge(fit_intercept=False, random_state=37),
            'lasso': lambda: Lasso(fit_intercept=False, random_state=37),
            'en': lambda: ElasticNet(l1_ratio=0.5, fit_intercept=False, random_state=37),
            'rf': lambda: RandomForestRegressor(random_state=37, n_jobs=-1)
        }

        if regressor in regressors:
            return regressors[regressor]
        return regressors['linear']

    def get_influence(c):
        r = get_regressor()()
        q = pd.DataFrame(StandardScaler().fit_transform(D[algo]), columns=D[algo].columns)
        q = q[c]

        r.fit(Z, q)

        if regressor == 'rf':
            f = r.feature_importances_
        else:
            f = r.coef_

        return pd.Series(np.abs(f), index=X.columns)

    Z = M[algo].named_steps['scaler'].transform(X)

    return pd.DataFrame({
            f'{algo}_C0': get_influence('C0'),
            f'{algo}_C1': get_influence('C1')
        })

def rescale(X):
    S = MinMaxScaler((20, 100)).fit_transform(X)

    S = pd.DataFrame(S, columns=X.columns, index=X.index) \
        .assign(**{
            f'__{X.columns[0]}': S[:,0]
        })

    return S

I = get_components('pca') \
    .join(get_components('kpca')) \
    .join(get_components('fa')) \
    .join(get_components('tsne')).T

I = rescale(I)
I

	mean radius	mean texture	mean perimeter	mean area	mean smoothness	mean compactness	mean concavity	mean concave points	mean symmetry	mean fractal dimension	...	worst texture	worst perimeter	worst area	worst smoothness	worst compactness	worst concavity	worst concave points	worst symmetry	worst fractal dimension	__mean radius
pca_C0	20.000000	27.660293	21.012388	20.089757	24.708053	25.028562	64.230320	100.000000	23.131311	20.070961	...	25.415234	31.177773	23.188636	23.694922	57.657200	40.778190	38.716474	25.768649	20.242635	20.000000
pca_C1	22.456687	25.707383	20.694835	57.455354	35.779462	21.683326	20.272224	20.750085	38.187873	100.000000	...	26.703584	33.359398	62.578362	51.705521	37.667882	38.185203	20.203508	33.673474	20.712339	22.456687
kpca_C0	20.124217	60.862211	20.000000	20.338962	34.834190	25.588299	100.000000	24.587450	27.726151	21.120664	...	31.514524	59.600710	35.243865	40.871446	57.364089	31.329845	21.401781	27.499165	20.917665	20.124217
kpca_C1	29.785557	37.624838	22.388116	93.877927	56.684593	22.079040	21.095430	20.598039	35.412102	74.147545	...	31.779264	65.516090	100.000000	47.628771	51.862636	34.163889	20.482895	34.958548	20.524924	29.785557
fa_C0	100.000000	20.000000	100.000000	100.000000	20.000000	20.000000	20.000000	20.000000	20.000000	20.000000	...	20.000000	20.000000	20.000000	20.000000	20.000000	20.000000	20.000000	20.000000	20.000000	100.000000
fa_C1	20.485784	29.111360	20.073381	22.051355	75.004853	100.000000	21.330962	20.438261	57.870181	49.368413	...	24.869753	20.951976	21.719272	65.038759	83.453114	100.000000	20.252925	33.431891	100.000000	20.485784
tsne_C0	20.133475	69.253239	20.226565	20.000000	52.425656	41.197356	29.660382	60.896868	24.332261	20.166627	...	80.989377	100.000000	40.055801	100.000000	100.000000	34.865060	100.000000	27.238558	20.766349	20.133475
tsne_C1	22.389117	100.000000	21.237619	41.932225	100.000000	30.457442	20.524996	21.595629	100.000000	44.820743	...	100.000000	43.921935	40.136060	89.301745	83.488993	67.899110	21.297724	100.000000	23.009203	22.389117

8 rows × 31 columns

In the table above, you can understand it by going down each colum or row. Going down each column, the value indicates the strength of influence of the original dimension on the new one. Going across each row, the value indicates how each column influences the component in magnitude (note that direction was removed by taking the absolute value of all coefficients).

For PCA, this regression of the new dimension on the old ones produces the eigenvectors!

4.7. Parallel coordinates

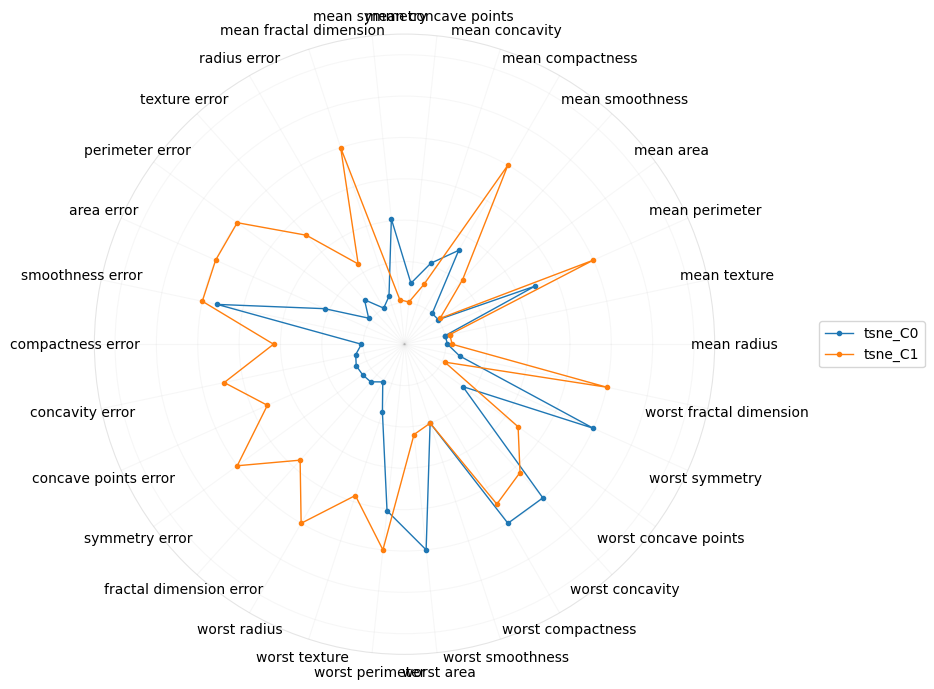
Now, we make the desperate attempt to visualize to see if there is any sensible higher-order meaning in the components. There’s a lot to look at, but for tSNE it seems the first component is about the “worst” features.

fig, ax = plt.subplots(figsize=(20, 5), dpi=100)

pd.plotting.parallel_coordinates(
    I.assign(y=I.index)[[True if i.endswith('C0') else False for i in I.index]] \
        .drop(columns=['__mean radius']),
    'y',
    color=sns.color_palette('tab10'),
    sort_labels=False,
    axvlines=False,
    ax=ax
)

ax.set_xticklabels(ax.get_xticklabels(), rotation=90)
ax.legend(loc='center left', bbox_to_anchor=(1, 0.5))

fig.tight_layout()

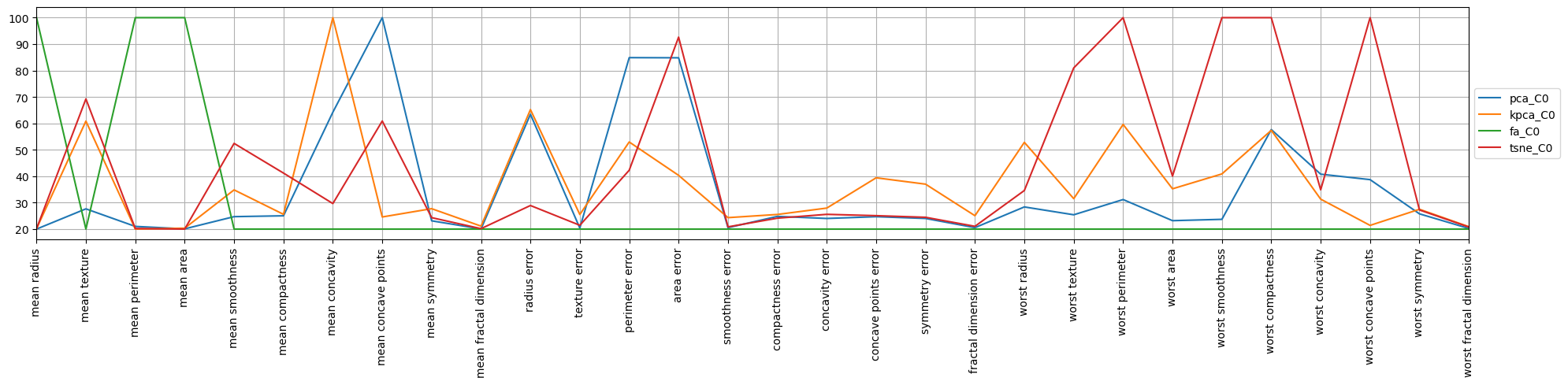
When looking at the second component for tSNE, it seems this component is about the “error” features.

fig, ax = plt.subplots(figsize=(20, 5), dpi=100)

pd.plotting.parallel_coordinates(
    I.assign(y=I.index)[[True if i.endswith('C1') else False for i in I.index]] \
        .drop(columns=['__mean radius']),
    'y',
    color=sns.color_palette('tab10'),
    sort_labels=False,
    axvlines=False,
    ax=ax
)

ax.set_xticklabels(ax.get_xticklabels(), rotation=90)
ax.legend(loc='center left', bbox_to_anchor=(1, 0.5))

fig.tight_layout()

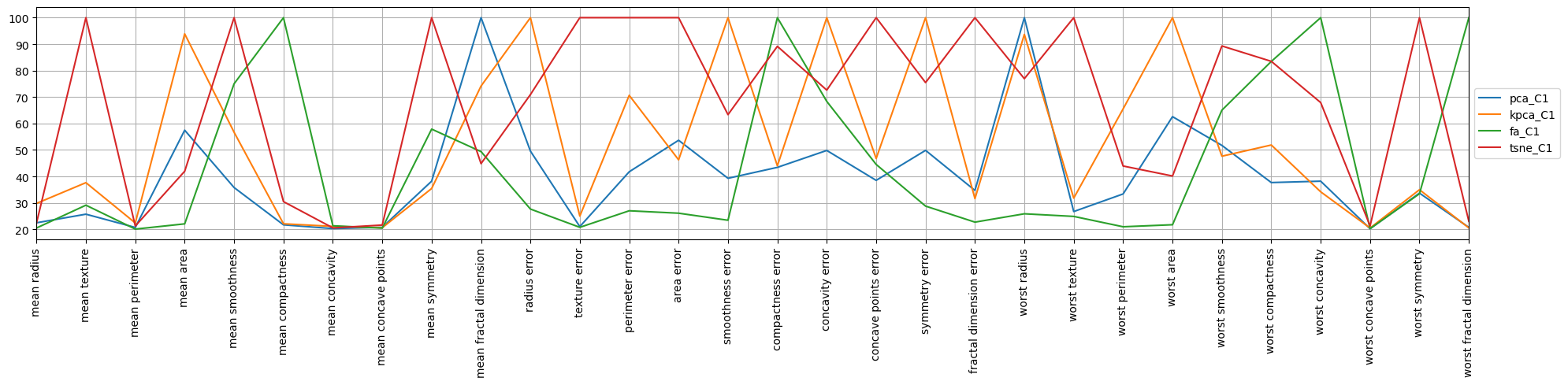
4.8. Radial plots

Perhaps radial plots can also give us a better intuition into what the concepts or higher-order meaning of the components are. The radial plot for tSNE gravitates towards the “worst” features, which confirms the interpretation from the parallel coordinate plot. Interestingly, for PCA, the first component is about the “mean” features.

fig, ax = plt.subplots(figsize=(10, 5), dpi=100)

pd.plotting.radviz(
    I.assign(y=I.index)[[True if i.endswith('C0') else False for i in I.index]] \
        .drop(columns=['__mean radius']),
    'y',
    color=sns.color_palette('tab10'),
    ax=ax
)
ax.axis('off')

fig.tight_layout()

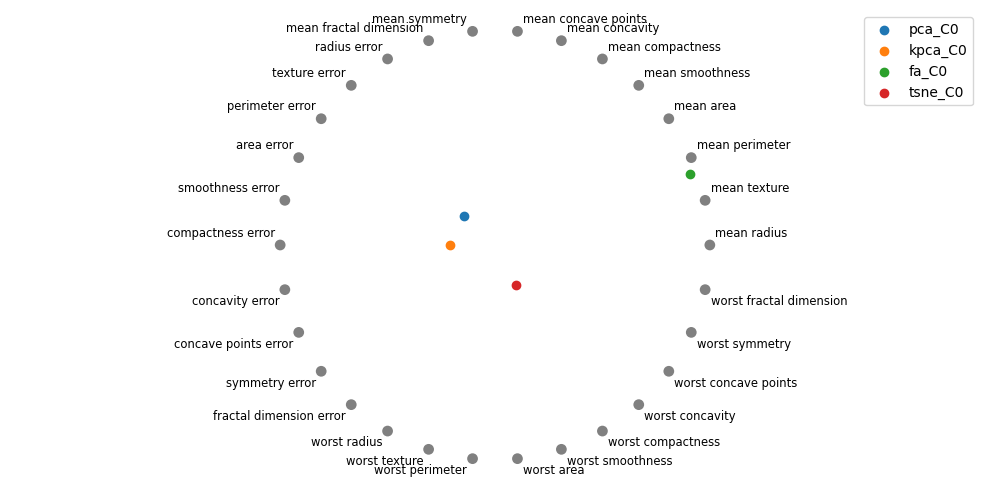
Let me know if you think there’s any signal with visualizing the coefficients of the features on the second component. It seems tSNE is moving towards the “error” features.

fig, ax = plt.subplots(figsize=(10, 5), dpi=100)

pd.plotting.radviz(
    I.assign(y=I.index)[[True if i.endswith('C1') else False for i in I.index]] \
        .drop(columns=['__mean radius']),
    'y',
    color=sns.color_palette('tab10'),
    ax=ax
)
ax.axis('off')

fig.tight_layout()

4.9. Polar plots

What about polar plots?

from matplotlib.text import Text

def plot_polar(X, markersize=3, linewidth=1, alpha=1.0):
    fig, ax = plt.subplots(subplot_kw={'projection': 'polar'}, figsize=(10, 7))

    d = X.shape[1]
    s = 360 / (d - 1)
    m = s * d + 1

    degrees = np.arange(s, m, s)
    radians = np.deg2rad(degrees)

    colors = sns.color_palette('tab10')
    for (name, r), color in zip(X.iterrows(), colors):
        ax.plot(
            radians,
            r,
            marker='o',
            markersize=markersize,
            linewidth=linewidth,
            color=color,
            alpha=alpha,
            label=name
        )

    ax.set_yticklabels([])
    ax.set_ylim(0, 150)
    ax.spines['polar'].set_alpha(0.1)

    x2l = {k: v for k, v in zip([0] + list(radians), X.columns[:X.shape[1]-1])}
    x_ticks = [x for x, _ in x2l.items()]
    x_labels = [Text(x, 0, label) for x, label in x2l.items()]

    ax.xaxis.set_ticks(x_ticks)
    ax.xaxis.set_ticklabels(x_labels)
    ax.legend(loc='center right', bbox_to_anchor=(1.35, 0.5))

    for gl in ax.xaxis.get_gridlines():
        gl.set_alpha(0.1)

    for gl in ax.yaxis.get_gridlines():
        gl.set_alpha(0.1)

    fig.tight_layout()

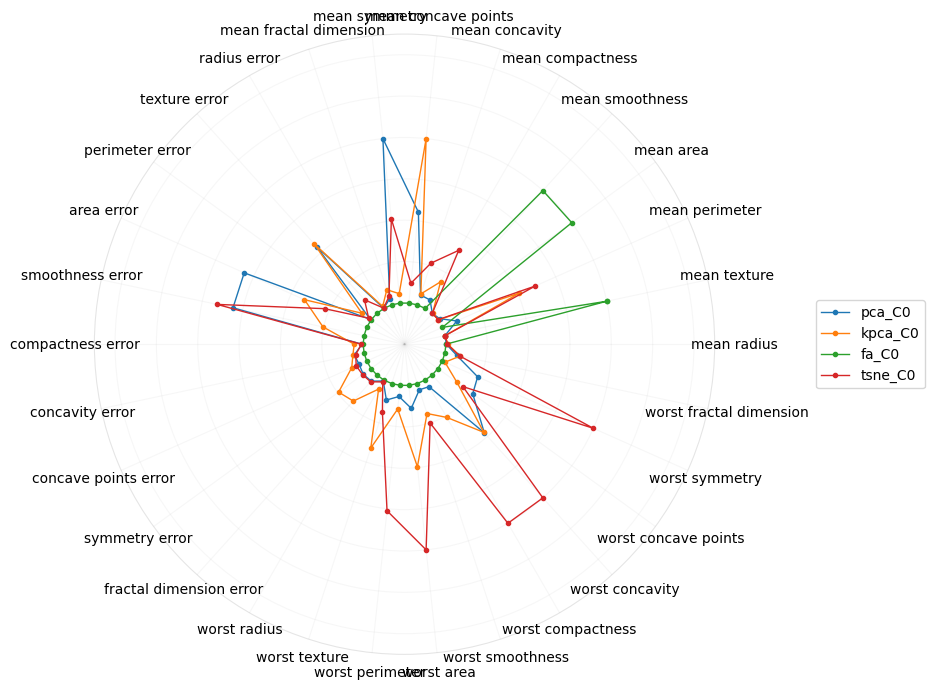
This polar plot is of the coefficients of the raw features on the projection into the first component.

plot_polar(I[[True if i.endswith('C0') else False for i in I.index]])

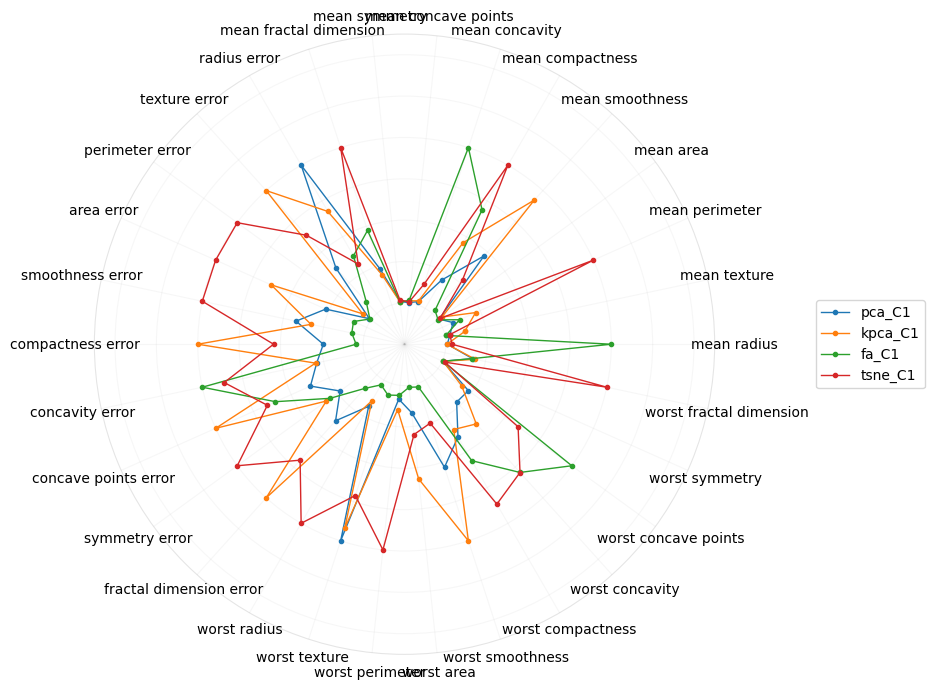
This polar plot is of the coefficients of the raw features on the projection into the second component.

plot_polar(I[[True if i.endswith('C1') else False for i in I.index]])

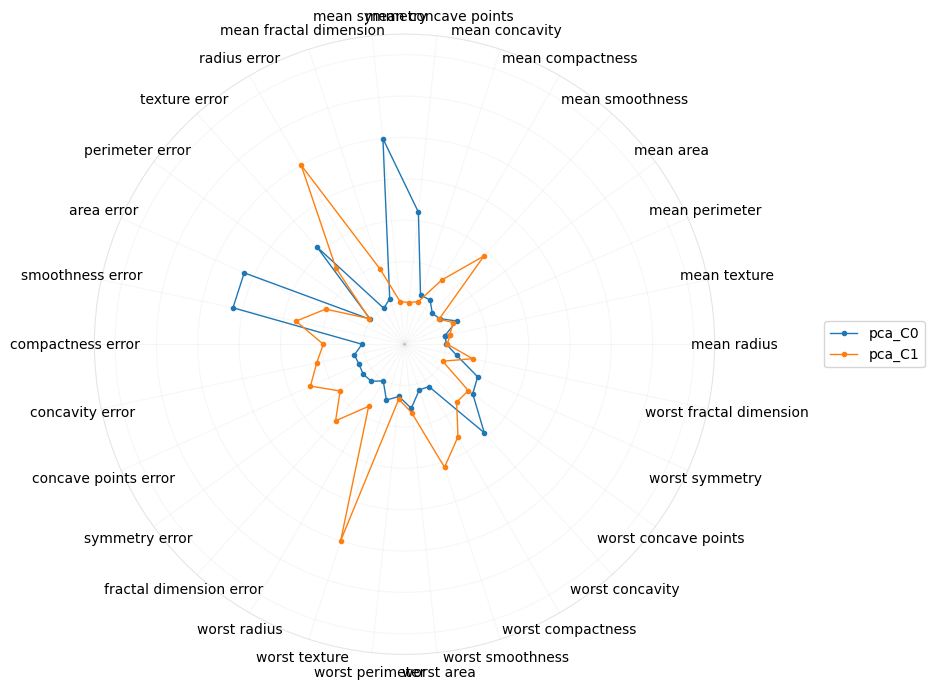
What if we just look at PCA?

plot_polar(I[[True if i.startswith('pca') else False for i in I.index]])

What if we just looked at kernel PCA?

plot_polar(I[[True if i.startswith('kpca') else False for i in I.index]])

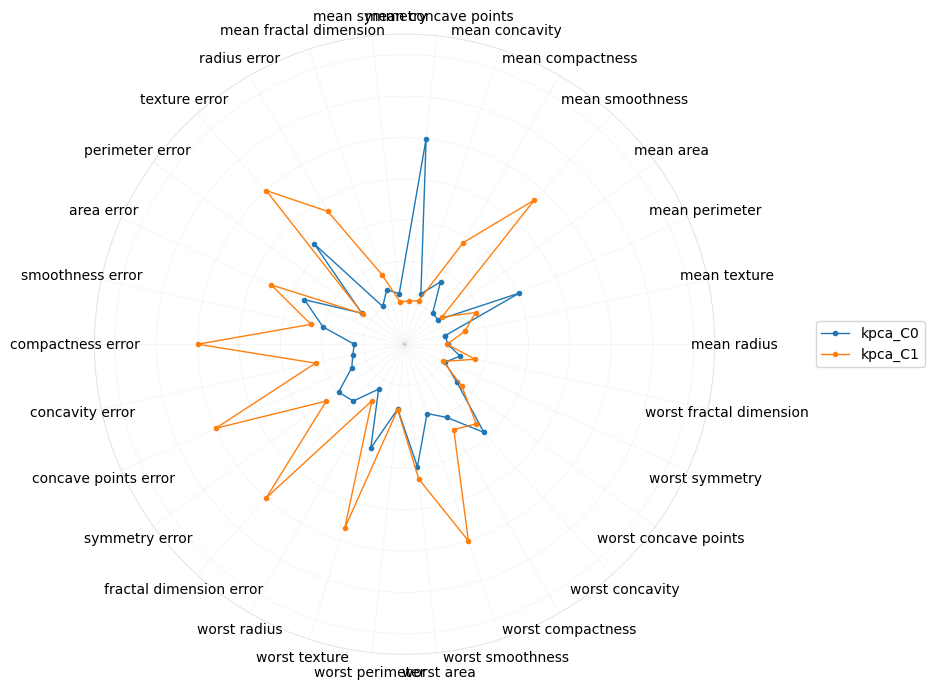
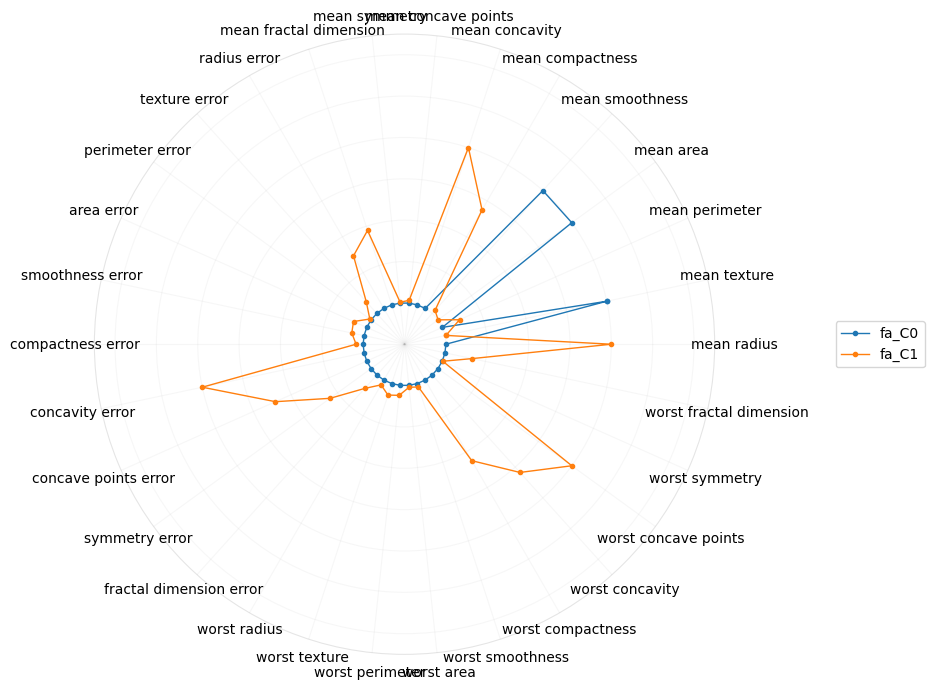
Or just factor analysis?

plot_polar(I[[True if i.startswith('fa') else False for i in I.index]])

And lastly, for tSNE.

plot_polar(I[[True if i.startswith('tsne') else False for i in I.index]])

4.10. Summary

Dimension reduction may be necessary to avoid certain problems associated with high-dimensionality. However, when reducing the dimensions, we are not simply doing “feature selection” (eg taking 30 features, in this case, and selecting only 2 from the 30). The dimension reduction techniques here are actually projecting the old/original dimensions into new ones, and those new (but fewer) dimensions have (higher-order) meaning, although it may not be easy to interpret exactly and precisely what those meanings may be.