6. Generating Random Bayesian Network
This notebook shows how to generate singly- and multi-connected Bayesian Belief Networks (BBNs). The algorithms are taken directly from here. When generating a BBN, you have to generate
the structure, which is a directed acyclic graph (DAG), and
the parameters, which are local probability models.
In this notebook, the parameters are assumed to take on the Dirichlet-Multinomial distribution. If you are wondering, a singly-connected BBN is one when, ignoring the directions of the edges in the DAG, there is at most one path between any two nodes. A multi-connected BBN is one that is not singly-connected (it is defined by the negation of a singly-connected BBN). The BBNs generated using this approach gaurantees the distribution of the BBNs are uniformly distributed (look at the paper for proofs, details, and benefits of having this property).
6.1. Generate the structure
Here, we generate the DAGs of a singly- and multi-connected BBNs. Note that when we visualize the DAGs, we do so by converting it to an undirected graph only because the layout algorithm is more aesthetically pleasing.
[1]:
import warnings
import networkx as nx
import numpy as np
import json
import matplotlib.pyplot as plt
from networkx.algorithms.dag import is_directed_acyclic_graph
from networkx.algorithms.shortest_paths.generic import shortest_path
np.random.seed(37)
def get_simple_ordered_tree(n):
"""
Generates a simple-ordered tree. The tree is just a
directed acyclic graph of n nodes with the structure
0 --> 1 --> .... --> n.
"""
g = nx.DiGraph()
for i in range(n):
g.add_node(i)
for i in range(n - 1):
g.add_edges_from([(i, i+1, {})])
return g
def convert_to_undirected_graph(g):
"""
Converts a directed acyclic graph (DAG) to an undirected graph.
We need to convert a DAG to an undirected one to use
some API calls to operate over the undirected graph. For example,
in checking for connectedness of a graph, the API has a method
to check for connectedness of an undirected graph, but not a
DAG.
"""
u = nx.Graph()
for n in g.nodes:
u.add_node(n)
for e in g.edges:
u.add_edges_from([(e[0], e[1], {})])
return u
def is_connected(g):
"""
Checks if a the directed acyclic graph is connected.
"""
u = convert_to_undirected_graph(g)
return nx.is_connected(u)
def get_random_node_pair(n):
"""
Randomly generates a pair of nodes.
"""
i = np.random.randint(0, n)
j = i
while j == i:
j = np.random.randint(0, n)
return i, j
def edge_exists(i, j, g):
"""
Checks if the edge i --> j exists in the graph, g.
"""
return j in list(g.successors(i))
def del_edge(i, j, g):
"""
Deletes the edge i --> j in the graph, g. The edge is only
deleted if this removal does NOT cause the graph to be
disconnected.
"""
if g.has_edge(i, j) is True:
g.remove_edge(i, j)
if is_connected(g) is False:
g.add_edges_from([(i, j, {})])
def add_edge(i, j, g):
"""
Adds an edge i --> j to the graph, g. The edge is only
added if this addition does NOT cause the graph to have
cycles.
"""
g.add_edges_from([(i, j, {})])
if is_directed_acyclic_graph(g) is False:
g.remove_edge(i, j)
def find_predecessor(i, j, g):
"""
Finds a predecessor, k, in the path between two nodes, i and j,
in the graph, g. We assume g is connected, and there is a
path between i and j (ignoring the direction of the edges).
We want to find a k, that is a parent of j, that is in
the path between i and j. In some cases, we may not find
such a k.
"""
parents = list(g.predecessors(j))
u = convert_to_undirected_graph(g)
for pa in parents:
try:
path = shortest_path(u, pa, i)
return pa
except:
pass
return None
def generate_multi_connected_structure(n, max_iter=10):
"""
Generates a multi-connected directed acyclic graph.
"""
g = get_simple_ordered_tree(n)
for it in range(max_iter):
i, j = get_random_node_pair(n)
if g.has_edge(i, j) is True:
del_edge(i, j, g)
else:
add_edge(i, j, g)
return g
def generate_singly_structure(n, max_iter=10):
"""
Generates a singly-connected directed acyclic graph.
"""
g = get_simple_ordered_tree(n)
counter = 0
for it in range(max_iter):
i, j = get_random_node_pair(n)
if g.has_edge(i, j) is True or g.has_edge(j, i) is True:
pass
else:
p = np.random.random()
k = find_predecessor(i, j, g)
if k is not None:
g.remove_edge(k, j)
if p < 0.5:
g.add_edges_from([(j, i, {})])
else:
g.add_edges_from([(i, j, {})])
if is_connected(g) is False:
g.add_edges_from([(k, j, {})])
if p < 0.5:
g.remove_edge(j, i)
else:
g.remove_edge(i, j)
return g
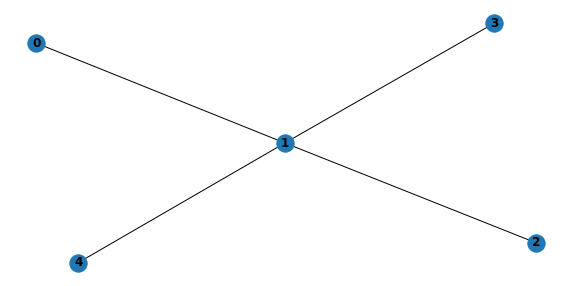
6.1.1. Generate DAG for singly-connected BBN
[2]:
with warnings.catch_warnings(record=True):
s = generate_singly_structure(5, 1000)
plt.figure(figsize=(10, 5))
plt.subplot(111)
nx.draw(convert_to_undirected_graph(s), with_labels=True, font_weight='bold')
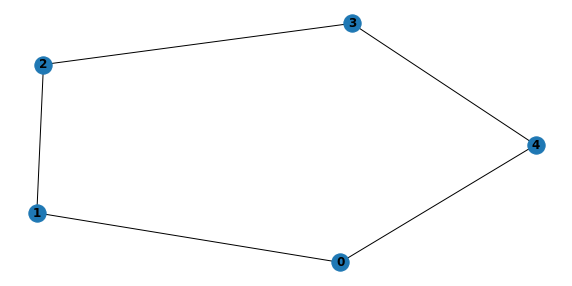
6.1.2. Generate DAG for multi-connected BBN
[3]:
with warnings.catch_warnings(record=True):
m = generate_multi_connected_structure(5, 10)
plt.figure(figsize=(10, 5))
plt.subplot(111)
nx.draw(convert_to_undirected_graph(m), with_labels=True, font_weight='bold')
6.2. Generate the parameters
Here, we generate parameters for the BBNs.
[4]:
from scipy.stats import dirichlet, multinomial
def generate_num_values(n, max_values=2):
"""
For each node, i, in the nodes, n, determine the number of values
the node (or equivalently, variable) has. Every node/variable in a
Bayesian Network should have 2 or more values. This generates
the number of values each variable will have. Each number will be
sampled uniformly.
"""
return np.array([max(np.random.randint(0, max_values) + 1, 2) for _ in range(n)])
def generate_alphas(n, max_alpha=10):
"""
Generate random number for the alpha's (the hyperparameters).
Each number will be in the range [1, max_alpha]. Each number will
be sampled uniformly.
"""
return [np.random.randint(1, max_alpha + 1) for i in range(n)]
def sample_dirichlet(n, max_alpha=10):
"""
Samples from the Dirichlet distribution to a produce
a probability vector of length n. The sum of each probability
in the probability vector should sum to 1.
"""
return np.array(dirichlet.rvs(generate_alphas(n, max_alpha))[0])
def get_num_parent_instantiations(parents, num_values):
num_pa_instantiations = 1
for pa in parents:
num_pa_values = num_values[pa]
num_pa_instantiations *= num_pa_values
return num_pa_instantiations
def generate_dirichlet_parameters(i, parents, num_values, max_alpha=10):
"""
Randomly and uniformly generate parameters for a node i. A matrix
of parameters will be returned. The matrix will represent the
condtional probability table of the node i. The matrix will have
the dimensions m (rows) by n (columns), m x n, where m is the
product of the domain sizes of the parents, and n is the domain
size of the node. The domain size is just the number of values
that a node (variable) has, which should always be greater than
or equal to 2.
"""
num_pa_instantiations = get_num_parent_instantiations(parents, num_values)
n = num_values[i]
cpt = []
for pa_instantiation in range(num_pa_instantiations):
probs = sample_dirichlet(n, max_alpha)
cpt.append(probs)
return np.array(cpt)
def generate_parameters(g, max_values=2, max_alpha=10):
"""
Generates parameters for each node in the graph, g.
A dictionary indexed by the node's id will give its
(sampled) parameters and its parents.
"""
num_nodes = len(list(g.nodes))
num_values = generate_num_values(num_nodes, max_values)
g_params = {}
for i in g.nodes:
parents = list(g.predecessors(i))
params = generate_dirichlet_parameters(i, parents, num_values, max_alpha)
g_params[i] = {
'parents': parents,
'params': params,
'shape': [get_num_parent_instantiations(parents, num_values), num_values[i]]
}
return g_params
6.2.1. Generate parameters for singly-connected BBN
[5]:
s_params = generate_parameters(s)
print(s_params)
{0: {'parents': [], 'params': array([[0.74174228, 0.25825772]]), 'shape': [1, 2]}, 1: {'parents': [2, 3, 0, 4], 'params': array([[0.50086958, 0.49913042],
[0.02647713, 0.97352287],
[0.42054028, 0.57945972],
[0.85369846, 0.14630154],
[0.22294388, 0.77705612],
[0.36867171, 0.63132829],
[0.86317661, 0.13682339],
[0.12457256, 0.87542744],
[0.50873009, 0.49126991],
[0.82929381, 0.17070619],
[0.67980646, 0.32019354],
[0.86189091, 0.13810909],
[0.8995967 , 0.1004033 ],
[0.53483643, 0.46516357],
[0.52939964, 0.47060036],
[0.83144941, 0.16855059]]), 'shape': [16, 2]}, 2: {'parents': [], 'params': array([[0.42051707, 0.57948293]]), 'shape': [1, 2]}, 3: {'parents': [], 'params': array([[0.80468897, 0.19531103]]), 'shape': [1, 2]}, 4: {'parents': [], 'params': array([[0.67431296, 0.32568704]]), 'shape': [1, 2]}}
6.2.2. Generate parameters for muti-connected BBN
[6]:
m_params = generate_parameters(m)
print(m_params)
{0: {'parents': [], 'params': array([[0.27733808, 0.72266192]]), 'shape': [1, 2]}, 1: {'parents': [0], 'params': array([[0.50940174, 0.49059826],
[0.99785858, 0.00214142]]), 'shape': [2, 2]}, 2: {'parents': [1, 3], 'params': array([[0.33727417, 0.66272583],
[0.79651078, 0.20348922],
[0.40652547, 0.59347453],
[0.88763038, 0.11236962]]), 'shape': [4, 2]}, 3: {'parents': [], 'params': array([[0.85069727, 0.14930273]]), 'shape': [1, 2]}, 4: {'parents': [3, 0], 'params': array([[0.68777784, 0.31222216],
[0.4609832 , 0.5390168 ],
[0.46319254, 0.53680746],
[0.10677866, 0.89322134]]), 'shape': [4, 2]}}
6.3. Persist (save) the Bayesian Belief Network
Here, we show how to save the BBN (the DAG and parameters). Note that we save it to a JSON file format. There are simply too many formats for BBNs, but the JSON format here has all the information you need to convert it to any other format.
[7]:
def to_json(g, params, pretty=True):
to_int_arr = lambda arr: [int(item) for item in arr]
j = {}
j['nodes'] = list(g.nodes)
j['edges'] = [{'pa': e[0], 'ch': e[1]} for e in g.edges]
j['parameters'] = [{'node': k,
'params': list(v['params'].flatten()),
'shape': to_int_arr(v['shape'])}
for k, v in params.items()]
if pretty:
return json.dumps(j, indent=2, sort_keys=False)
return json.dumps(j)
6.3.1. Persist singly-connected BBN
[8]:
s_json = to_json(s, s_params)
print(s_json)
with open('./output/singly-connected.json', 'w') as fhandle:
fhandle.write(to_json(s, s_params, pretty=True))
{
"nodes": [
0,
1,
2,
3,
4
],
"edges": [
{
"pa": 0,
"ch": 1
},
{
"pa": 2,
"ch": 1
},
{
"pa": 3,
"ch": 1
},
{
"pa": 4,
"ch": 1
}
],
"parameters": [
{
"node": 0,
"params": [
0.7417422803682197,
0.25825771963178046
],
"shape": [
1,
2
]
},
{
"node": 1,
"params": [
0.5008695756264835,
0.4991304243735164,
0.026477131905188734,
0.9735228680948113,
0.42054028327937387,
0.579459716720626,
0.8536984622587769,
0.14630153774122318,
0.22294387680535926,
0.7770561231946408,
0.3686717093409431,
0.6313282906590567,
0.8631766076552874,
0.13682339234471266,
0.1245725606108167,
0.8754274393891833,
0.5087300903407761,
0.49126990965922374,
0.8292938143560679,
0.1707061856439322,
0.6798064596245497,
0.32019354037545045,
0.8618909056718044,
0.13810909432819546,
0.8995966961793681,
0.10040330382063184,
0.5348364275608116,
0.4651635724391883,
0.5293996424146508,
0.47060035758534935,
0.8314494130139252,
0.16855058698607464
],
"shape": [
16,
2
]
},
{
"node": 2,
"params": [
0.42051706936960864,
0.5794829306303914
],
"shape": [
1,
2
]
},
{
"node": 3,
"params": [
0.8046889692800407,
0.19531103071995928
],
"shape": [
1,
2
]
},
{
"node": 4,
"params": [
0.6743129580736985,
0.3256870419263015
],
"shape": [
1,
2
]
}
]
}
6.3.2. Persist multi-connected BBN
[9]:
m_json = to_json(m, m_params)
print(m_json)
with open('./output/multi-connected.json', 'w') as fhandle:
fhandle.write(to_json(m, m_params, pretty=True))
{
"nodes": [
0,
1,
2,
3,
4
],
"edges": [
{
"pa": 0,
"ch": 1
},
{
"pa": 0,
"ch": 4
},
{
"pa": 1,
"ch": 2
},
{
"pa": 3,
"ch": 4
},
{
"pa": 3,
"ch": 2
}
],
"parameters": [
{
"node": 0,
"params": [
0.2773380778096063,
0.7226619221903937
],
"shape": [
1,
2
]
},
{
"node": 1,
"params": [
0.5094017382812316,
0.4905982617187683,
0.9978585783502765,
0.002141421649723624
],
"shape": [
2,
2
]
},
{
"node": 2,
"params": [
0.3372741656699353,
0.6627258343300647,
0.7965107759562755,
0.20348922404372444,
0.40652547264228284,
0.5934745273577172,
0.8876303836604758,
0.11236961633952422
],
"shape": [
4,
2
]
},
{
"node": 3,
"params": [
0.8506972724905534,
0.14930272750944656
],
"shape": [
1,
2
]
},
{
"node": 4,
"params": [
0.6877778356657721,
0.31222216433422784,
0.4609831964438165,
0.5390168035561835,
0.4631925375186775,
0.5368074624813227,
0.10677865814938657,
0.8932213418506135
],
"shape": [
4,
2
]
}
]
}
6.4. All-in-one (AIO) example
Here’s a simple AIO example of generating a singly-connected BBN and its corresponding JSON.
[10]:
g = generate_singly_structure(5, 1000)
p = generate_parameters(g)
j = to_json(g, p)