9. Log-linear Models for Three-way Tables

Log-linear modeling is a type of analysis to understand the association between categorical variables. This approach uses regression to achieve its objective. However, the use of log-linear modeling is often multi-step, requires the production and comparison of many models and necessitates reflection on the tradeoff between goodness-of-fit GoF and model parsimony, degrees-of-freedom DoF. Log-linear modeling differs from logistic or multinomial regression in that the latter will typically pick one of the categorical variables to be the dependent variable (conditional distribution of the dependent variable given the independent variables); in log-linear models, the dependent variable comes from the counts of the contingency table induced by the variables (joint distribution). As such, a very good way to understand log-linear modeling is to understand contingency tables.

In a three-way contingency table, we have 3 categorical variables, denoted as A, B and C and whose levels (values) are indexed as I, J and K, correspondingly. The log of the count \(\mu_{ijk} = n \pi_{ijk}\) (\(n\) is the sum of all the counts and \(\pi_{ijk} = \dfrac{n_{ijk}}{n}\)) is in a linear relationship to A, B and C in a finite number of ways, one of which is optimal and what we are trying to find using log-linear modeling. Here are some ways that \(\mu_{ijk}\) may be related to A, B and C. (Remember that \(\mu_{ijk}\) is the product of the corresponding marginals divided by the total).

  • independence: A, B and C are all independent, denoted as (A, B, C)

    • \(\log{\mu_{ijk}} = \lambda + \lambda_i^A + \lambda_j^B + \lambda_k^C\)

  • joint independence: AB are jointly independent of C (AB, C); AC are jointly independent of B (AC, B); BC are jointly independent of A (BC, A)

    • \(\log{\mu_{ijk}} = \lambda + \lambda_i^A + \lambda_j^B + \lambda_k^C + \lambda_{jk}^{AB}\)

    • \(\log{\mu_{ijk}} = \lambda + \lambda_i^A + \lambda_j^B + \lambda_k^C + \lambda_{jk}^{AC}\)

    • \(\log{\mu_{ijk}} = \lambda + \lambda_i^A + \lambda_j^B + \lambda_k^C + \lambda_{jk}^{BC}\)

  • conditional independence: A and B are independent given C (AC, BC); A and C are independent given B (AB, BC); B and C are independent give A (AB, AC)

    • \(\log{\mu_{ijk}} = \lambda + \lambda_i^A + \lambda_j^B + \lambda_k^C + \lambda_{ik}^{AC} + \lambda_{jk}^{BC}\)

    • \(\log{\mu_{ijk}} = \lambda + \lambda_i^A + \lambda_j^B + \lambda_k^C + \lambda_{ij}^{AB} + \lambda_{jk}^{BC}\)

    • \(\log{\mu_{ijk}} = \lambda + \lambda_i^A + \lambda_j^B + \lambda_k^C + \lambda_{ij}^{AB} + \lambda_{ik}^{AC}\)

  • homogeneous association: there is no three way interaction (AB, AC, BC)

    • \(\log{\mu_{ijk}} = \lambda + \lambda_i^A + \lambda_j^B + \lambda_k^C + \lambda_{ij}^{AB} + \lambda_{ik}^{AC} + \lambda_{jk}^{BC}\)

  • saturated: there are main, pairwise and three-way effects (ABC)

    • \(\log{\mu_{ijk}} = \lambda + \lambda_i^A + \lambda_j^B + \lambda_k^C + \lambda_{ij}^{AB} + \lambda_{ik}^{AC} + \lambda_{jk}^{BC} + \lambda_{ijk}^{ABC}\)

The models above actually represent a Poisson regression model. Each cell count \(n_{ijk}\) is assumed to be Poisson distributed \(n_{ijk} \sim \operatorname{Pois}(\mu_{ijk})\). Thus, \(\lambda\) is the intercept and \(\lambda_i^A\), \(\lambda_j^B\), \(\lambda_k^C\) and so on are coefficients.

Each of these models will have a DoF and GoF associated with them. The GoF can be the log-likelihood of the model (higher is better) or the deviance \(G^2\) (lower is better). If we wanted to know the association between A, B and C, we can start from the independence model and move forward towards the saturated model (adding terms), or, we can start from the saturated model and move backward towards the independence model (remove terms). What is removed or added depends on how the GoF and DoF changes; we must strike a balance between GoF and model parsimony. We typically compare models using a likelihood ratio test based on \(G^2\).

Lastly, the log-linear models above have graphical representation. Each log-linear model above asserts associations between the three variables.

9.1. Load data

This data is about UC-Berkely admissions from 1970. There are 3 categorical variables.

  • A: admission

  • B: sex

  • C: department

[1]:

import pandas as pd

df = pd.read_csv('./data/berkeley-admission.csv')
df.shape

[1]:

(24, 4)

The three-way contingency table looks like the following.

[2]:

pd.crosstab(df['department'], [df['sex'], df['admission']], values=df['n'], aggfunc=lambda x: x)

[2]:
sex Female Male
admission Admitted Rejected Admitted Rejected
department
A 89 19 512 313
B 17 8 353 207
C 202 391 120 205
D 131 244 139 279
E 94 299 53 138
F 24 317 22 351

We will use log-linear models to understand the relationship between these three variables.

9.2. Complete independence model (A, B, C)

\(\log{\mu_{ijk}} = \lambda + \lambda_i^A + \lambda_j^B + \lambda_k^C\)

[3]:

import networkx as nx
import matplotlib.pyplot as plt

plt.style.use('ggplot')

def draw_graph(g):
    fig, ax = plt.subplots(figsize=(5, 5))

    pos = {
        'A': (200, 250),
        'B': (150, 230),
        'C': (250, 230)
    }

    params = {
        'node_color': 'r',
        'node_size': 350,
        'node_shape': 's',
        'alpha': 0.5,
        'pos': pos,
        'ax': ax
    }
    _ = nx.drawing.nx_pylab.draw_networkx_nodes(g, **params)

    params = {
        'font_size': 15,
        'font_color': 'k',
        'font_family': 'monospace',
        'pos': pos,
        'ax': ax
    }
    _ = nx.drawing.nx_pylab.draw_networkx_labels(g, **params)

    params = {
        'width': 1.5,
        'alpha': 0.5,
        'edge_color': 'b',
        'arrowsize': 20,
        'pos': pos,
        'ax': ax
    }
    _ = nx.drawing.nx_pylab.draw_networkx_edges(g, **params)


g = nx.Graph()
g.add_node('A')
g.add_node('B')
g.add_node('C')

draw_graph(g)
_images/log-linear-model_7_0.png 
[4]:

from patsy import dmatrices
import statsmodels.api as sm

dept_levels = ['F', 'A', 'B', 'C', 'D', 'E']

y, X = dmatrices('n ~ admission + sex + C(department, levels=dept_levels)', df, return_type='dataframe')
sm.GLM(y, X, family=sm.families.Poisson()).fit().summary()

[4]:
Generalized Linear Model Regression Results
Dep. Variable: n No. Observations: 24
Model: GLM Df Residuals: 16
Model Family: Poisson Df Model: 7
Link Function: log Scale: 1.0000
Method: IRLS Log-Likelihood: -1128.1
Date: Wed, 09 Mar 2022 Deviance: 2097.1
Time: 12:13:30 Pearson chi2: 2.00e+03
No. Iterations: 5
Covariance Type: nonrobust
coef std err z P>|z| [0.025 0.975]
Intercept 4.7208 0.046 103.681 0.000 4.632 4.810
admission[T.Rejected] 0.4562 0.031 14.956 0.000 0.396 0.516
sex[T.Male] 0.3832 0.030 12.660 0.000 0.324 0.443
C(department, levels=dept_levels)[T.A] 0.2675 0.050 5.380 0.000 0.170 0.365
C(department, levels=dept_levels)[T.B] -0.1993 0.056 -3.573 0.000 -0.309 -0.090
C(department, levels=dept_levels)[T.C] 0.2513 0.050 5.036 0.000 0.154 0.349
C(department, levels=dept_levels)[T.D] 0.1049 0.052 2.034 0.042 0.004 0.206
C(department, levels=dept_levels)[T.E] -0.2010 0.056 -3.602 0.000 -0.310 -0.092

9.3. Joint independence

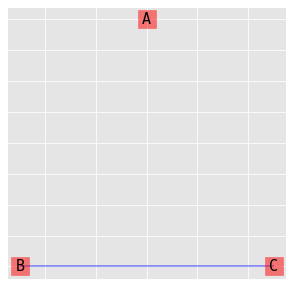
9.3.1. (A, BC)

\(\log{\mu_{ijk}} = \lambda + \lambda_i^A + \lambda_j^B + \lambda_k^C + \lambda_{jk}^{BC}\)

[5]:

g = nx.Graph()
g.add_node('A')
g.add_node('B')
g.add_node('C')
g.add_edge('B', 'C')

draw_graph(g)
_images/log-linear-model_11_0.png 
[6]:

y, X = dmatrices('n ~ admission + sex + C(department, levels=dept_levels) + sex * C(department, levels=dept_levels)', df, return_type='dataframe')
sm.GLM(y, X, family=sm.families.Poisson()).fit().summary()

[6]:
Generalized Linear Model Regression Results
Dep. Variable: n No. Observations: 24
Model: GLM Df Residuals: 11
Model Family: Poisson Df Model: 12
Link Function: log Scale: 1.0000
Method: IRLS Log-Likelihood: -517.91
Date: Wed, 09 Mar 2022 Deviance: 876.74
Time: 12:13:30 Pearson chi2: 797.
No. Iterations: 7
Covariance Type: nonrobust
coef std err z P>|z| [0.025 0.975]
Intercept 4.8849 0.057 85.279 0.000 4.773 4.997
admission[T.Rejected] 0.4562 0.031 14.956 0.000 0.396 0.516
sex[T.Male] 0.0897 0.075 1.197 0.231 -0.057 0.237
C(department, levels=dept_levels)[T.A] -1.1498 0.110 -10.413 0.000 -1.366 -0.933
C(department, levels=dept_levels)[T.B] -2.6130 0.207 -12.611 0.000 -3.019 -2.207
C(department, levels=dept_levels)[T.C] 0.5533 0.068 8.141 0.000 0.420 0.687
C(department, levels=dept_levels)[T.D] 0.0950 0.075 1.270 0.204 -0.052 0.242
C(department, levels=dept_levels)[T.E] 0.1419 0.074 1.918 0.055 -0.003 0.287
sex[T.Male]:C(department, levels=dept_levels)[T.A] 1.9436 0.127 15.325 0.000 1.695 2.192
sex[T.Male]:C(department, levels=dept_levels)[T.B] 3.0194 0.218 13.869 0.000 2.593 3.446
sex[T.Male]:C(department, levels=dept_levels)[T.C] -0.6911 0.102 -6.784 0.000 -0.891 -0.491
sex[T.Male]:C(department, levels=dept_levels)[T.D] 0.0189 0.103 0.183 0.855 -0.184 0.221
sex[T.Male]:C(department, levels=dept_levels)[T.E] -0.8112 0.116 -7.010 0.000 -1.038 -0.584

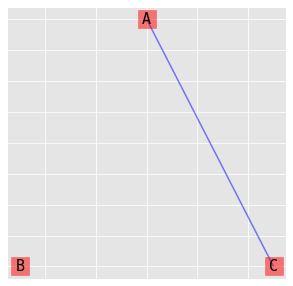
9.3.2. (B, AC)

\(\log{\mu_{ijk}} = \lambda + \lambda_i^A + \lambda_j^B + \lambda_k^C + \lambda_{ik}^{AC}\)

[7]:

g = nx.Graph()
g.add_node('A')
g.add_node('B')
g.add_node('C')
g.add_edge('A', 'C')

draw_graph(g)
_images/log-linear-model_14_0.png 
[8]:

y, X = dmatrices('n ~ admission + sex + C(department, levels=dept_levels) + admission * C(department, levels=dept_levels)', df, return_type='dataframe')
sm.GLM(y, X, family=sm.families.Poisson()).fit().summary()

[8]:
Generalized Linear Model Regression Results
Dep. Variable: n No. Observations: 24
Model: GLM Df Residuals: 11
Model Family: Poisson Df Model: 12
Link Function: log Scale: 1.0000
Method: IRLS Log-Likelihood: -700.56
Date: Wed, 09 Mar 2022 Deviance: 1242.1
Time: 12:13:30 Pearson chi2: 1.08e+03
No. Iterations: 6
Covariance Type: nonrobust
coef std err z P>|z| [0.025 0.975]
Intercept 2.9256 0.149 19.696 0.000 2.634 3.217
admission[T.Rejected] 2.6756 0.152 17.553 0.000 2.377 2.974
sex[T.Male] 0.3832 0.030 12.660 0.000 0.324 0.443
C(department, levels=dept_levels)[T.A] 2.5700 0.153 16.799 0.000 2.270 2.870
C(department, levels=dept_levels)[T.B] 2.0849 0.156 13.336 0.000 1.778 2.391
C(department, levels=dept_levels)[T.C] 1.9459 0.158 12.345 0.000 1.637 2.255
C(department, levels=dept_levels)[T.D] 1.7698 0.160 11.095 0.000 1.457 2.082
C(department, levels=dept_levels)[T.E] 1.1618 0.169 6.877 0.000 0.831 1.493
admission[T.Rejected]:C(department, levels=dept_levels)[T.A] -3.2691 0.167 -19.567 0.000 -3.597 -2.942
admission[T.Rejected]:C(department, levels=dept_levels)[T.B] -3.2185 0.175 -18.402 0.000 -3.561 -2.876
admission[T.Rejected]:C(department, levels=dept_levels)[T.C] -2.0600 0.167 -12.306 0.000 -2.388 -1.732
admission[T.Rejected]:C(department, levels=dept_levels)[T.D] -2.0145 0.170 -11.860 0.000 -2.347 -1.682
admission[T.Rejected]:C(department, levels=dept_levels)[T.E] -1.5861 0.180 -8.822 0.000 -1.939 -1.234

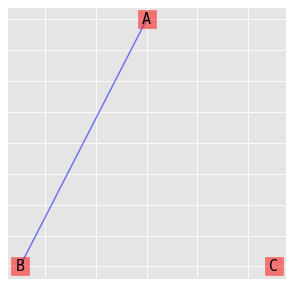
9.3.3. (C, AB)

\(\log{\mu_{ijk}} = \lambda + \lambda_i^A + \lambda_j^B + \lambda_k^C + \lambda_{ij}^{AB}\)

[9]:

g = nx.Graph()
g.add_node('A')
g.add_node('B')
g.add_node('C')
g.add_edge('A', 'B')

draw_graph(g)
_images/log-linear-model_17_0.png 
[10]:

y, X = dmatrices('n ~ admission + sex + C(department, levels=dept_levels) + admission * sex', df, return_type='dataframe')
sm.GLM(y, X, family=sm.families.Poisson()).fit().summary()

[10]:
Generalized Linear Model Regression Results
Dep. Variable: n No. Observations: 24
Model: GLM Df Residuals: 15
Model Family: Poisson Df Model: 8
Link Function: log Scale: 1.0000
Method: IRLS Log-Likelihood: -1081.2
Date: Wed, 09 Mar 2022 Deviance: 2003.4
Time: 12:13:30 Pearson chi2: 1.75e+03
No. Iterations: 5
Covariance Type: nonrobust
coef std err z P>|z| [0.025 0.975]
Intercept 4.4756 0.055 82.056 0.000 4.369 4.583
admission[T.Rejected] 0.8305 0.051 16.357 0.000 0.731 0.930
sex[T.Male] 0.7667 0.051 14.952 0.000 0.666 0.867
C(department, levels=dept_levels)[T.A] 0.2675 0.050 5.380 0.000 0.170 0.365
C(department, levels=dept_levels)[T.B] -0.1993 0.056 -3.573 0.000 -0.309 -0.090
C(department, levels=dept_levels)[T.C] 0.2513 0.050 5.036 0.000 0.154 0.349
C(department, levels=dept_levels)[T.D] 0.1049 0.052 2.034 0.042 0.004 0.206
C(department, levels=dept_levels)[T.E] -0.2010 0.056 -3.602 0.000 -0.310 -0.092
admission[T.Rejected]:sex[T.Male] -0.6112 0.064 -9.567 0.000 -0.736 -0.486

9.4. Conditional independence

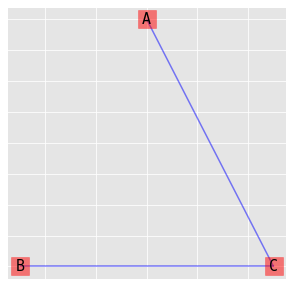
9.4.1. (AC, BC)

\(\log{\mu_{ijk}} = \lambda + \lambda_i^A + \lambda_j^B + \lambda_k^C + \lambda_{ik}^{AC} + \lambda_{jk}^{BC}\)

[11]:

g = nx.Graph()
g.add_node('A')
g.add_node('B')
g.add_node('C')
g.add_edge('A', 'C')
g.add_edge('B', 'C')

draw_graph(g)
_images/log-linear-model_21_0.png 
[12]:

y, X = dmatrices('n ~ admission + sex + C(department, levels=dept_levels) + admission * C(department, levels=dept_levels) + sex * C(department, levels=dept_levels)', df, return_type='dataframe')
sm.GLM(y, X, family=sm.families.Poisson()).fit().summary()

[12]:
Generalized Linear Model Regression Results
Dep. Variable: n No. Observations: 24
Model: GLM Df Residuals: 6
Model Family: Poisson Df Model: 17
Link Function: log Scale: 1.0000
Method: IRLS Log-Likelihood: -90.376
Date: Wed, 09 Mar 2022 Deviance: 21.686
Time: 12:13:30 Pearson chi2: 19.9
No. Iterations: 7
Covariance Type: nonrobust
coef std err z P>|z| [0.025 0.975]
Intercept 3.0896 0.153 20.253 0.000 2.791 3.389
admission[T.Rejected] 2.6756 0.152 17.553 0.000 2.377 2.974
sex[T.Male] 0.0897 0.075 1.197 0.231 -0.057 0.237
C(department, levels=dept_levels)[T.A] 1.1527 0.182 6.334 0.000 0.796 1.509
C(department, levels=dept_levels)[T.B] -0.3289 0.254 -1.297 0.195 -0.826 0.168
C(department, levels=dept_levels)[T.C] 2.2479 0.164 13.687 0.000 1.926 2.570
C(department, levels=dept_levels)[T.D] 1.7599 0.168 10.447 0.000 1.430 2.090
C(department, levels=dept_levels)[T.E] 1.5047 0.176 8.559 0.000 1.160 1.849
admission[T.Rejected]:C(department, levels=dept_levels)[T.A] -3.2691 0.167 -19.567 0.000 -3.597 -2.942
admission[T.Rejected]:C(department, levels=dept_levels)[T.B] -3.2185 0.175 -18.402 0.000 -3.561 -2.876
admission[T.Rejected]:C(department, levels=dept_levels)[T.C] -2.0600 0.167 -12.306 0.000 -2.388 -1.732
admission[T.Rejected]:C(department, levels=dept_levels)[T.D] -2.0145 0.170 -11.860 0.000 -2.347 -1.682
admission[T.Rejected]:C(department, levels=dept_levels)[T.E] -1.5861 0.180 -8.822 0.000 -1.939 -1.234
sex[T.Male]:C(department, levels=dept_levels)[T.A] 1.9436 0.127 15.325 0.000 1.695 2.192
sex[T.Male]:C(department, levels=dept_levels)[T.B] 3.0194 0.218 13.869 0.000 2.593 3.446
sex[T.Male]:C(department, levels=dept_levels)[T.C] -0.6911 0.102 -6.784 0.000 -0.891 -0.491
sex[T.Male]:C(department, levels=dept_levels)[T.D] 0.0189 0.103 0.183 0.855 -0.184 0.221
sex[T.Male]:C(department, levels=dept_levels)[T.E] -0.8112 0.116 -7.010 0.000 -1.038 -0.584

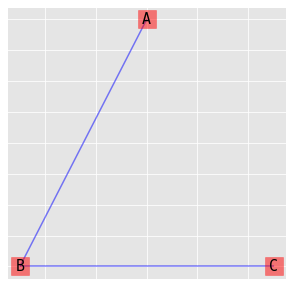
9.4.2. (AB, BC)

\(\log{\mu_{ijk}} = \lambda + \lambda_i^A + \lambda_j^B + \lambda_k^C + \lambda_{ij}^{AB} + \lambda_{jk}^{BC}\)

[13]:

g = nx.Graph()
g.add_node('A')
g.add_node('B')
g.add_node('C')
g.add_edge('A', 'B')
g.add_edge('B', 'C')

draw_graph(g)
_images/log-linear-model_24_0.png 
[14]:

y, X = dmatrices('n ~ admission + sex + C(department, levels=dept_levels) + admission * sex + sex * C(department, levels=dept_levels)', df, return_type='dataframe')
sm.GLM(y, X, family=sm.families.Poisson()).fit().summary()

[14]:
Generalized Linear Model Regression Results
Dep. Variable: n No. Observations: 24
Model: GLM Df Residuals: 10
Model Family: Poisson Df Model: 13
Link Function: log Scale: 1.0000
Method: IRLS Log-Likelihood: -471.04
Date: Wed, 09 Mar 2022 Deviance: 783.02
Time: 12:13:31 Pearson chi2: 715.
No. Iterations: 7
Covariance Type: nonrobust
coef std err z P>|z| [0.025 0.975]
Intercept 4.6396 0.065 71.737 0.000 4.513 4.766
admission[T.Rejected] 0.8305 0.051 16.357 0.000 0.731 0.930
sex[T.Male] 0.4731 0.086 5.528 0.000 0.305 0.641
C(department, levels=dept_levels)[T.A] -1.1498 0.110 -10.413 0.000 -1.366 -0.933
C(department, levels=dept_levels)[T.B] -2.6130 0.207 -12.611 0.000 -3.019 -2.207
C(department, levels=dept_levels)[T.C] 0.5533 0.068 8.141 0.000 0.420 0.687
C(department, levels=dept_levels)[T.D] 0.0950 0.075 1.270 0.204 -0.052 0.242
C(department, levels=dept_levels)[T.E] 0.1419 0.074 1.918 0.055 -0.003 0.287
admission[T.Rejected]:sex[T.Male] -0.6112 0.064 -9.567 0.000 -0.736 -0.486
sex[T.Male]:C(department, levels=dept_levels)[T.A] 1.9436 0.127 15.325 0.000 1.695 2.192
sex[T.Male]:C(department, levels=dept_levels)[T.B] 3.0194 0.218 13.869 0.000 2.593 3.446
sex[T.Male]:C(department, levels=dept_levels)[T.C] -0.6911 0.102 -6.784 0.000 -0.891 -0.491
sex[T.Male]:C(department, levels=dept_levels)[T.D] 0.0189 0.103 0.183 0.855 -0.184 0.221
sex[T.Male]:C(department, levels=dept_levels)[T.E] -0.8112 0.116 -7.010 0.000 -1.038 -0.584

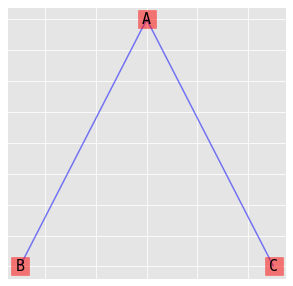
9.4.3. (AB, AC)

\(\log{\mu_{ijk}} = \lambda + \lambda_i^A + \lambda_j^B + \lambda_k^C + \lambda_{ij}^{AB} + \lambda_{ik}^{AC}\)

[15]:

g = nx.Graph()
g.add_node('A')
g.add_node('B')
g.add_node('C')
g.add_edge('A', 'B')
g.add_edge('A', 'C')

draw_graph(g)
_images/log-linear-model_27_0.png 
[16]:

y, X = dmatrices('n ~ admission + sex + C(department, levels=dept_levels) + admission * sex + admission * C(department, levels=dept_levels)', df, return_type='dataframe')
sm.GLM(y, X, family=sm.families.Poisson()).fit().summary()

[16]:
Generalized Linear Model Regression Results
Dep. Variable: n No. Observations: 24
Model: GLM Df Residuals: 10
Model Family: Poisson Df Model: 13
Link Function: log Scale: 1.0000
Method: IRLS Log-Likelihood: -653.70
Date: Wed, 09 Mar 2022 Deviance: 1148.3
Time: 12:13:31 Pearson chi2: 1.02e+03
No. Iterations: 6
Covariance Type: nonrobust
coef std err z P>|z| [0.025 0.975]
Intercept 2.6804 0.152 17.688 0.000 2.383 2.977
admission[T.Rejected] 3.0500 0.158 19.335 0.000 2.741 3.359
sex[T.Male] 0.7667 0.051 14.952 0.000 0.666 0.867
C(department, levels=dept_levels)[T.A] 2.5700 0.153 16.799 0.000 2.270 2.870
C(department, levels=dept_levels)[T.B] 2.0849 0.156 13.336 0.000 1.778 2.391
C(department, levels=dept_levels)[T.C] 1.9459 0.158 12.345 0.000 1.637 2.255
C(department, levels=dept_levels)[T.D] 1.7698 0.160 11.095 0.000 1.457 2.082
C(department, levels=dept_levels)[T.E] 1.1618 0.169 6.877 0.000 0.831 1.493
admission[T.Rejected]:sex[T.Male] -0.6112 0.064 -9.567 0.000 -0.736 -0.486
admission[T.Rejected]:C(department, levels=dept_levels)[T.A] -3.2691 0.167 -19.567 0.000 -3.597 -2.942
admission[T.Rejected]:C(department, levels=dept_levels)[T.B] -3.2185 0.175 -18.402 0.000 -3.561 -2.876
admission[T.Rejected]:C(department, levels=dept_levels)[T.C] -2.0600 0.167 -12.306 0.000 -2.388 -1.732
admission[T.Rejected]:C(department, levels=dept_levels)[T.D] -2.0145 0.170 -11.860 0.000 -2.347 -1.682
admission[T.Rejected]:C(department, levels=dept_levels)[T.E] -1.5861 0.180 -8.822 0.000 -1.939 -1.234

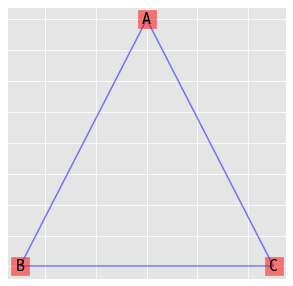
9.5. Homogeneous model

\(\log{\mu_{ijk}} = \lambda + \lambda_i^A + \lambda_j^B + \lambda_k^C + \lambda_{ij}^{AB} + \lambda_{ik}^{AC} + \lambda_{jk}^{BC}\)

[17]:

g = nx.Graph()
g.add_node('A')
g.add_node('B')
g.add_node('C')
g.add_edge('A', 'B')
g.add_edge('A', 'C')
g.add_edge('B', 'C')

draw_graph(g)
_images/log-linear-model_30_0.png 
[18]:

y, X = dmatrices('n ~ (admission + sex + C(department, levels=dept_levels))**2', df, return_type='dataframe')
sm.GLM(y, X, family=sm.families.Poisson()).fit().summary()

[18]:
Generalized Linear Model Regression Results
Dep. Variable: n No. Observations: 24
Model: GLM Df Residuals: 5
Model Family: Poisson Df Model: 18
Link Function: log Scale: 1.0000
Method: IRLS Log-Likelihood: -89.642
Date: Wed, 09 Mar 2022 Deviance: 20.217
Time: 12:13:31 Pearson chi2: 18.8
No. Iterations: 7
Covariance Type: nonrobust
coef std err z P>|z| [0.025 0.975]
Intercept 3.1364 0.157 20.011 0.000 2.829 3.444
admission[T.Rejected] 2.6256 0.158 16.646 0.000 2.316 2.935
sex[T.Male] -0.0018 0.106 -0.017 0.987 -0.210 0.207
C(department, levels=dept_levels)[T.A] 1.1359 0.182 6.242 0.000 0.779 1.493
C(department, levels=dept_levels)[T.B] -0.3422 0.253 -1.351 0.177 -0.839 0.154
C(department, levels=dept_levels)[T.C] 2.2233 0.165 13.484 0.000 1.900 2.546
C(department, levels=dept_levels)[T.D] 1.7466 0.168 10.387 0.000 1.417 2.076
C(department, levels=dept_levels)[T.E] 1.4814 0.176 8.407 0.000 1.136 1.827
admission[T.Rejected]:sex[T.Male] 0.0978 0.081 1.210 0.226 -0.061 0.256
admission[T.Rejected]:C(department, levels=dept_levels)[T.A] -3.3057 0.170 -19.448 0.000 -3.639 -2.973
admission[T.Rejected]:C(department, levels=dept_levels)[T.B] -3.2621 0.179 -18.247 0.000 -3.613 -2.912
admission[T.Rejected]:C(department, levels=dept_levels)[T.C] -2.0442 0.168 -12.177 0.000 -2.373 -1.715
admission[T.Rejected]:C(department, levels=dept_levels)[T.D] -2.0156 0.170 -11.865 0.000 -2.349 -1.683
admission[T.Rejected]:C(department, levels=dept_levels)[T.E] -1.5676 0.180 -8.688 0.000 -1.921 -1.214
sex[T.Male]:C(department, levels=dept_levels)[T.A] 2.0011 0.136 14.747 0.000 1.735 2.267
sex[T.Male]:C(department, levels=dept_levels)[T.B] 3.0759 0.223 13.802 0.000 2.639 3.513
sex[T.Male]:C(department, levels=dept_levels)[T.C] -0.6634 0.104 -6.357 0.000 -0.868 -0.459
sex[T.Male]:C(department, levels=dept_levels)[T.D] 0.0459 0.106 0.434 0.664 -0.161 0.253
sex[T.Male]:C(department, levels=dept_levels)[T.E] -0.7932 0.117 -6.799 0.000 -1.022 -0.565

9.6. Saturated model

The saturated model is not estimated due to perfect separation.

\(\log{\mu_{ijk}} = \lambda + \lambda_i^A + \lambda_j^B + \lambda_k^C + \lambda_{ij}^{AB} + \lambda_{ik}^{AC} + \lambda_{jk}^{BC} + \lambda_{ijk}^{ABC}\)

9.7. Model Selection

With model selection, we can perform a likelihood ratio test between any two models.

[19]:

def get_deviance(m, f):
    y, X = dmatrices(f, df, return_type='dataframe')
    r = sm.GLM(y, X, family=sm.families.Poisson()).fit()

    return {'model': m, 'df': r.df_resid, 'deviance': r.deviance}

formulas = {
    '(A, B, C)': 'n ~ admission + sex + C(department, levels=dept_levels)',
    '(A, BC)': 'n ~ admission + sex + C(department, levels=dept_levels) + sex * C(department, levels=dept_levels)',
    '(B, AC)': 'n ~ admission + sex + C(department, levels=dept_levels) + admission * C(department, levels=dept_levels)',
    '(C, AB)': 'n ~ admission + sex + C(department, levels=dept_levels) + admission * sex',
    '(AC, BC)': 'n ~ admission + sex + C(department, levels=dept_levels) + admission * C(department, levels=dept_levels) + sex * C(department, levels=dept_levels)',
    '(AB, BC)': 'n ~ admission + sex + C(department, levels=dept_levels) + admission * sex + sex * C(department, levels=dept_levels)',
    '(AB, AC)': 'n ~ admission + sex + C(department, levels=dept_levels) + admission * sex + admission * C(department, levels=dept_levels)',
    '(AB, AC, BC)': 'n ~ (admission + sex + C(department, levels=dept_levels))**2'
}

result_df = pd.DataFrame([get_deviance(m, f) for m, f in formulas.items()]).set_index('model')
result_df

[19]:
df deviance
model
(A, B, C) 16 2097.116655
(A, BC) 11 876.743972
(B, AC) 11 1242.058607
(C, AB) 15 2003.390913
(AC, BC) 6 21.685924
(AB, BC) 10 783.018230
(AB, AC) 10 1148.332865
(AB, AC, BC) 5 20.217417

Here are are comparing (AB, BC) \(H_0\) vs (AB, AC, BC) \(H_{\alpha}\). Since p < 0.01, we reject \(H_0\).

[20]:

from scipy.stats import chi2

chi_sq = result_df.loc['(AB, BC)'].deviance - result_df.loc['(AB, AC, BC)'].deviance
dof = result_df.loc['(AB, BC)'].df - result_df.loc['(AB, AC, BC)'].df

1 - chi2.cdf(chi_sq, dof)

[20]:

0.0

Here are are comparing (AC, BC) \(H_0\) vs (AB, AC, BC) \(H_{\alpha}\). Since p = 0.23, we fail to reject \(H_0\).

[21]:

chi_sq = result_df.loc['(AC, BC)'].deviance - result_df.loc['(AB, AC, BC)'].deviance
dof = result_df.loc['(AC, BC)'].df - result_df.loc['(AB, AC, BC)'].df

1 - chi2.cdf(chi_sq, dof)

[21]:

0.22558143086494165

What is the model (AC, BC) telling us? Remember, A is admission, B is sex and C is department. So, that we favor (AC, BC) as the best model, admission and sex are independent given department; meaning, there is no relationship between admission and sex given that we know which department they applied to, and the marginal association is spurious.