1. Generating Normally Distributed Values
This notebook shows how to generate values from a normal (Gaussian) distribution. There are three main algorithms that are covered.
Box-Muller transform
Marsaglia-Tsang
Ziggurat
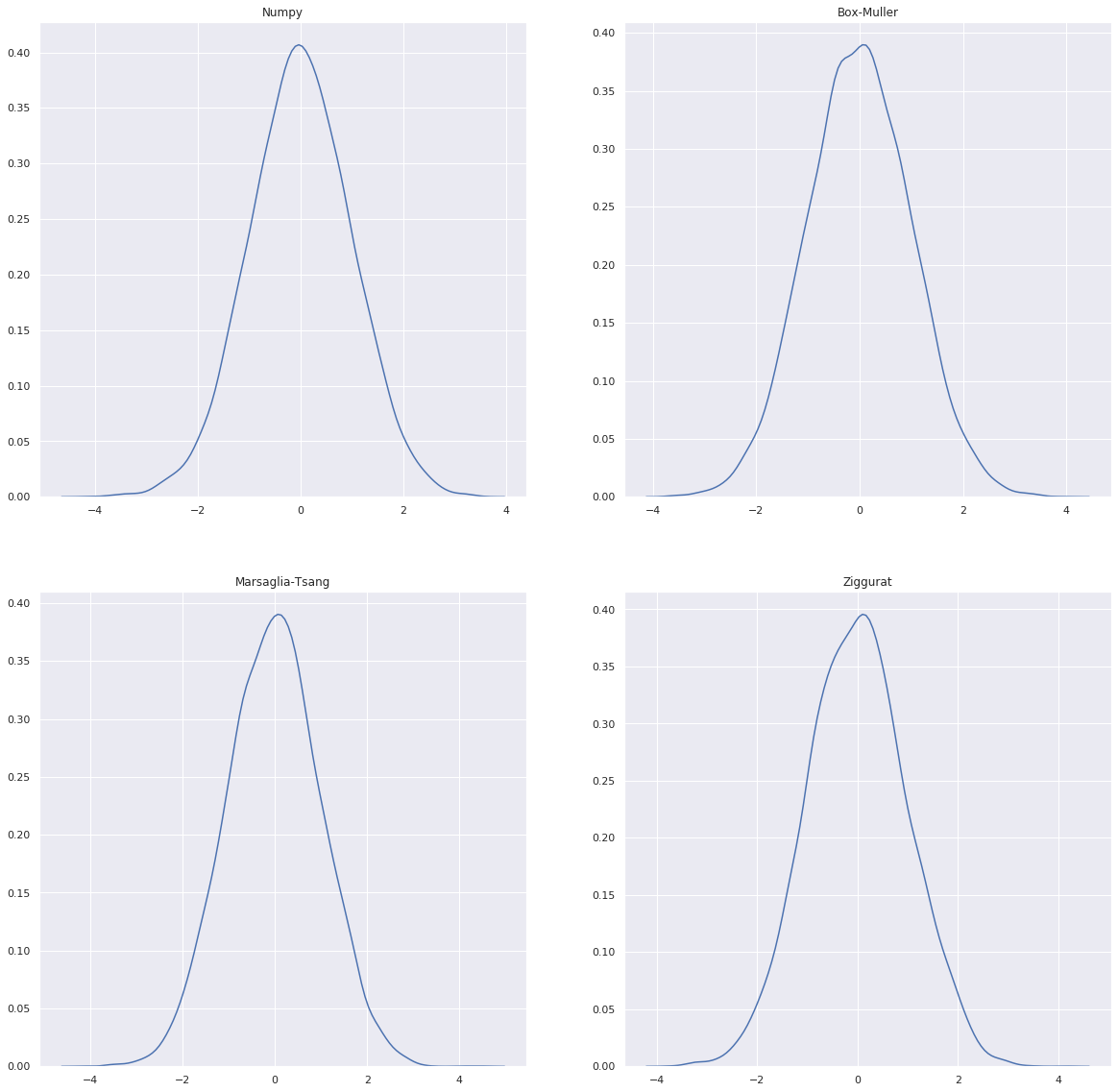
The Box-Muller and Marsaglia-Tsang algorithms are very similar in shape and form. Box-Muller operates in polar coordinates while Marsaglia-Tsang operates in Cartesian coordinates. All three algorithms sample for points and test for rejection/acceptance. Box-Muller and Marsaglia-Tsang sample for points within the unit square while Ziggurat samples based on stacked rectangles covering half of the normal distribution. The Ziggurat algorithm is the fastest, followed by Marsaglia-Tsang and then Box-Muller.
We simply implement all three algorithms in this notebook and compare the outputs to numpy.
1.1. Box-Mueller method
[1]:
%matplotlib inline
import sys
import time
import ctypes
import numpy as np
import seaborn as sns
import matplotlib.pyplot as plt
np.random.seed(37)
sns.set(color_codes=True)
num_samples = 10000
def box_muller(m, std):
epsilon = sys.float_info.min
two_pi = 2.0 * np.pi
u1 = 0.0
u2 = 0.0
while True:
u1 = np.random.rand()
u2 = np.random.rand()
if u1 > epsilon:
break
z0 = np.sqrt(-2.0 * np.log(u1)) * np.cos(two_pi * u2)
z1 = np.sqrt(-2.0 * np.log(u1)) * np.sin(two_pi * u2)
return m + std * z0
1.2. Marsaglia-Tsang method
[2]:
def marsaglia_tsang(m, std):
u = 0.0
v = 0.0
s = 0.0
while True:
u = np.random.rand() * 2.0 - 1.0
v = np.random.rand() * 2.0 - 1.0
s = np.power(u, 2.0) + np.power(v, 2.0)
if 0.0 < s and s <= 1.0:
break
z = np.sqrt(-2.0 * np.log(s) / s)
return m + std * u * z
1.3. Ziggurat method
Although the Ziggurat algorithm is the fastest, it is not the easiest to understand or implement. The implementation here is a translation from JavaScript (which was itself a translation from C, dead link). Note all the low-level bitwise operations.
[3]:
class Ziggurat(object):
def __init__(self, mean=0.0, std=1.0, seed=37):
self.mean = mean
self.std = std
self.wn = np.array([0.0 for i in range(128)], dtype=np.float)
self.fn = np.array([0.0 for i in range(128)], dtype=np.float)
self.kn = np.array([0.0 for i in range(128)], dtype=np.float)
self.jsr = 123456789 ^ (seed if seed is not None else int(time.time()))
m1 = 2147483648.0
dn = 3.442619855899
tn = dn
vn = 9.91256303526217e-3
q = vn / np.exp(-0.5 * dn * dn)
self.kn[0] = np.floor((dn / q) * m1)
self.kn[1] = 0
self.wn[0] = q / m1
self.wn[127] = dn / m1
self.fn[0] = 1.0
self.fn[127] = np.exp(-0.5 * dn * dn)
i = 126
while i >= 1:
dn = np.sqrt(-2.0 * np.log(vn / dn + np.exp(-0.5 * dn * dn)))
self.kn[i+1] = np.floor((dn / tn) * m1)
tn = dn
self.fn[i] = np.exp(-0.5 * dn * dn)
self.wn[i] = dn / m1
i -= 1
def shr3(self):
def rshift(val, n):
if val >= 0:
return ctypes.c_int(val >> n).value
else:
return ctypes.c_int((val+0x100000000) >> n).value
jz = self.jsr
jzr = self.jsr
jzr = ctypes.c_int(jzr ^ (jzr << 13)).value
jzr = ctypes.c_int(jzr ^ rshift(jzr, 17)).value
jzr = ctypes.c_int(jzr ^ (jzr << 5)).value
self.jsr = jzr
return ctypes.c_int((jz+jzr) | 0).value
def uni(self):
return 0.5 * (1.0 + self.shr3() / -np.power(2, 31))
def uni_safe(self):
while True:
u = self.uni()
if 0 != u:
return u
def rnorm(self):
hz = self.shr3()
iz = hz & 127
return self.mean + self.std * (hz * self.wn[iz] if np.abs(hz) < self.kn[iz] else self.nfix(hz, iz))
def nfix(self, hz, iz):
r = 3.442619855899
r1 = 1.0 / r
x = 0
y = 0
while True:
x = hz * self.wn[iz]
if iz == 0:
x = -np.log(self.uni_safe()) * r1
y = -np.log(self.uni_safe())
while True:
x = -np.log(self.uni_safe()) * r1
y = -np.log(self.uni_safe())
if y + y >= x * x:
break
return r + x if hz > 0 else -r - x
if self.fn[iz] + self.uni() * (self.fn[iz-1] - self.fn[iz]) < np.exp(-0.5 * x * x):
return x
hz = self.shr3()
iz = hz & 127
if np.abs(hz) < self.kn[iz]:
return hz * self.wn[iz]
1.4. Sampling
[4]:
num_samples = 10000
mean = 0
std = 1
zigg = Ziggurat(mean=mean, std=std)
np_samples = np.random.normal(mean, std, num_samples)
bm_samples = np.array([box_muller(mean, std) for _ in range(num_samples)])
mt_samples = np.array([marsaglia_tsang(mean, std) for _ in range(num_samples)])
zi_samples = np.array([zigg.rnorm() for _ in range(num_samples)])
1.5. Visualize the densities
[5]:
fig, ax = plt.subplots(2, 2, figsize=(20, 20), sharex=False, sharey=False)
sns.kdeplot(np_samples, ax=ax[0, 0])
sns.kdeplot(bm_samples, ax=ax[0, 1])
sns.kdeplot(mt_samples, ax=ax[1, 0])
sns.kdeplot(zi_samples, ax=ax[1, 1])
ax[0, 0].set_title('Numpy')
ax[0, 1].set_title('Box-Muller')
ax[1, 0].set_title('Marsaglia-Tsang')
ax[1, 1].set_title('Ziggurat')
[5]:
Text(0.5, 1.0, 'Ziggurat')