2. d-separation, Active Paths

Direction-dependent separation, or d-separation, is a rule for reading conditional independencies off a directed acyclic graph, DAG. The utility of d-separation is that it can determine if two mutually exclusive sets of variables, \(X\) and \(Y\), are independent give a third \(Z\). The output of d-separation is true when \(X\) and \(Y\) are independent given \(Z\), denoted as \(I(X,Y|Z)\), and false when \(X\) and \(Y\) are dependent given \(Z\), denoted as \(D(X,Y|Z)\). If the output of d-separation is true, then \(X\) and \(Y\) are said to be d-separated given \(Z\); likewise, if the output of d-separation is false, then \(X\) and \(Y\) are said to be d-connected given \(Z\).

Let’s motivate the importance of d-separation. Let’s say we want to know if the treatment of an illness, \(T\), and the outcome of the illness, \(E\), are independent given race, \(R\). We want to know which of the following are true.

• \(I(T,E|R)\)

• \(D(T,E|R)\)

If \(T\) and \(E\) given \(R\) are d-separated, then once we know \(R\), \(T\) and \(E\) are no longer related. If \(T\) and \(E\) given \(R\) are d-connected, then when we know \(R\), \(T\) and \(E\) become related.

2.1. Graph example

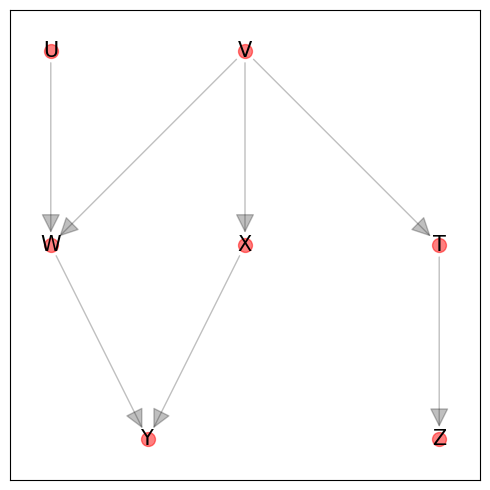
Here is a graph taken from this most excellent video tutorial on d-separation exercises. We will be using this graph to show some d-separation queries.

import networkx as nx
from collections import namedtuple

Graph = namedtuple('Graph', 'u, d')

def get_edges(s):
    edges = s.split('\n')
    edges = map(lambda line: line.split('->'), edges)
    edges = map(lambda tokens: tuple([t.strip() for t in tokens]), edges)
    edges = list(edges)

    return edges

def get_directed_graph(edges):
    g = nx.DiGraph()
    g.add_edges_from(edges)

    return g

def get_undirected_graph(edges):
    g = nx.Graph()
    g.add_edges_from(edges)

    return g

def get_graph(s):
    e = get_edges(s)

    d = get_directed_graph(e)
    u = get_undirected_graph(e)
    g = Graph(u, d)

    return g

s = '''
U -> W
V -> W
V -> X
V -> T
W -> Y
X -> Y
T -> Z
'''.strip()

g = get_graph(s)

import matplotlib.pyplot as plt

pos = nx.nx_agraph.graphviz_layout(g.d, prog='dot')

fig, ax = plt.subplots(figsize=(5, 5))

nx.draw_networkx_nodes(
    G=g.d,
    pos=pos,
    ax=ax,
    node_size=100,
    alpha=0.5,
    node_color='red'
)

nx.draw_networkx_labels(
    G=g.d,
    pos=pos,
    ax=ax,
    font_size=15,
    font_color='black',
    alpha=1.0
)

nx.draw_networkx_edges(
    G=g.d,
    pos=pos,
    alpha=0.25,
    arrowsize=30,
    ax=ax
)

fig.tight_layout()

2.2. Algorithm

Here’s an algorithm to determine if \(X\) and \(Y\) are d-separated given \(Z\).

• Input:

  • \(G\): DAG

  • \(X\): start node

  • \(Y\): end node

  • \(Z\): evidence nodes

• Output: True or False

• Find all paths, \(P\), between \(X\) and \(Y\)

• For each path \(p\) in \(P\)

  • if \(p\) is active, return False

• return True

In the algorithm above, if we find any path in \(G\) between \(X\) and \(Y\) (given \(Z\)) that is active, then \(X\) and \(Y\) are d-connected; if we cannot find any active path between \(X\) and \(Y\) (given \(Z\)) in \(G\) then they are d-separated. The idea of an active and inactive path comes through understanding the configuration of triplets in a DAG. In general, there are 3 types of triplet configurations.

• serial: \(X \rightarrow Z \rightarrow Y\) (causal chain)

• diverging: \(X \leftarrow Z \rightarrow Y\) (common cause)

• converging: \(X \rightarrow Z \leftarrow Y\) (common effect, also called a v-structure)

For the serial and diverging configurations, without evidence of \(Z\), the configurations are active; if we do have evidence of \(Z\), then the serial and diverging configurations are inactive. The converging configuration is unique; without evidence of \(Z\), the configuration is inactive, and with evidence, the configuration is active. Active and inactive is about opening or blocking information, respectively.

A path between \(X\) and \(Y\) (given \(Z\)) is said to be active if all contiguous triplets are active (like a conjunctive boolean AND). If at least one of the contiguous triplets in the path is inactive, then the path is inactive (like a disjunctive boolean OR).

def get_all_paths(g, start, stop):
    return nx.all_simple_paths(g.u, start, stop)

def get_path_triplets(path):
    if len(path) < 3:
        return [path]
    else:
        return [path[i:i+3] for i in range(0, len(path) - 2)]

def get_triplet_type(g, x, z, y):
    x_children = set(g.d.successors(x))
    z_children = set(g.d.successors(z))
    y_children = set(g.d.successors(y))

    if z in x_children and y in z_children:
        return 'serial'
    if z in y_children and x in z_children:
        return 'serial'
    if x in z_children and y in z_children:
        return 'diverging'
    if z in x_children and z in y_children:
        return 'converging'
    raise Exception(f'cannot determine triplet configuration: x={x}, z={z}, y={y}')

def is_active_triplet(g, x, z, y, evidence=set()):
    triplet_type = get_triplet_type(g, x, z, y)

    if triplet_type in {'serial', 'diverging'}:
        if z in evidence:
            return False
        else:
            return True
    else:
        z_set = nx.descendants(g.d, z)
        z_set.add(z)

        if len(z_set & evidence) > 0:
            return True
        else:
            return False

def is_active_path(g, path, evidence=set()):
    if len(path) < 3:
        if path[0] in evidence or path[-1] in evidence:
            return False
        else:
            return True

    path_triplets = get_path_triplets(path)

    for x, z, y in path_triplets:
        if not is_active_triplet(g, x, z, y, evidence):
            return False
    return True

def is_d_separated(g, x, y, evidence=set()):
    paths = list(get_all_paths(g, x, y))

    if len(paths) < 1:
        return True

    for path in get_all_paths(g, x, y):
        if is_active_path(g, path, evidence):
            return False
    return True

2.3. Examples

Below are some exercise examples to query for d-separation based on the algorithm and code above.

2.3.1. Example 1

is_d_separated(g, 'V', 'Z')

False

2.3.2. Example 2

is_d_separated(g, 'V', 'Z', {'T'})

True

2.3.3. Example 3

is_d_separated(g, 'U', 'V')

True

2.3.4. Example 4

is_d_separated(g, 'U', 'V', {'W'})

False

2.3.5. Example 5

is_d_separated(g, 'U', 'V', {'X'})

True

2.3.6. Example 6

is_d_separated(g, 'U', 'V', {'Y'})

False

2.3.7. Example 7

is_d_separated(g, 'U', 'V', {'Z'})

True

2.3.8. Example 8

is_d_separated(g, 'W', 'X')

False

2.3.9. Example 9

is_d_separated(g, 'X', 'T', {'V'})

True

2.3.10. Example 10

is_d_separated(g, 'X', 'W', {'U'})

False

2.3.11. Example 11

is_d_separated(g, 'Y', 'Z')

False

2.3.12. Example 12

is_d_separated(g, 'Y', 'Z', 'T')

True

2.3.13. Example 13

is_d_separated(g, 'Y', 'Z', {'X'})

False

2.3.14. Example 14

is_d_separated(g, 'Y', 'Z', {'V'})

True

2.3.15. Example 15

is_d_separated(g, 'W', 'Z', {'V'})

True

2.3.16. Example 16

is_d_separated(g, 'U', 'Z')

True

2.3.17. Example 17

is_d_separated(g, 'U', 'Z', {'Y'})

False

2.3.18. Additional examples

is_d_separated(g, 'U', 'W')

False

is_d_separated(g, 'U', 'W', {'U'})

True

is_d_separated(g, 'U', 'W', {'W'})

True